Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Le plan est muni d'un repère orthonormé, déterminer une équation du cercle $\mathcal{C}$ dans chaque cas.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
- $\mathcal{C}$ a pour centre $C(2;1)$ et pour rayon 3
Équation d'un cercle
Dans un repère orthonormé, le cercle de centre $C(x_C;y_C)$ et de rayon $r$ a pour équation $(x-x_C)^2+(y-y_C)^2=r^2$$(x-x_C)^2+(y-y_C)^2=r^2 \Longleftrightarrow (x-2)^2+(y-1)^2=3^2 $
- $\mathcal{C}$ a pour centre $C(-3;2)$ et pour rayon $\sqrt{3}$
- $\mathcal{C}$ a pour diamètre $[AB]$ avec $A(2;3)$ et $B(-4;1)$
On peut soit calculer les coordonnées du centre du cercle et son rayon $r=\dfrac{AB}{2}$
soit utiliser le fait que $M(x;y) \in \mathcal{C} \Longleftrightarrow \overrightarrow{AM}. \overrightarrow{BM}=0$Soit $C$ le milieu de $[AB]$
$\begin{cases} x_C =\dfrac{x_A+x_B}{2}=\dfrac{2-4}{2}=-1 \\ y_C =\dfrac{y_A+y_B}{2}=\dfrac{3+1}{2}=2 \end{cases}$
donc $C(-1;2)$ est le milieu de $[AB]$ donc le centre du cercle $\mathcal{C}$
$AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}=\sqrt{(-6)^2+(-2)^2}=\sqrt{40}=2\sqrt{10}$
donc le cercle $\mathcal{C}$ a pour rayon $r=\dfrac{2\sqrt{10}}{2}=\sqrt{10}$
On a donc pour équation du cercle: $(x-(-1))^2+(y-2)^2=\sqrt{10}^2$
Avec le produit scalaire:
Soit $M(x:y)$ un point du cercle $\mathcal{C}$
$\begin{cases} x_{ \overrightarrow{AM} } =x_M-x_A=x-2 \\ y_{ \overrightarrow{AM} } =y_M-y_A=y-3 \end{cases}$
donc $ \overrightarrow{AM}(x-2;y-3)$
$\begin{cases} x_{ \overrightarrow{BM}} =x_M-x_B=x-(-4)=x+4 \\ y_{ \overrightarrow{BM} } =y_M-y_B=y-1 \end{cases}$
donc $ \overrightarrow{BM}(x+4;y-1)$
$M \in \mathcal{C} \Longleftrightarrow \overrightarrow{AM}. \overrightarrow{BM}=0$
$\phantom{M\in\mathcal{C}} \Longleftrightarrow (x-2)(x+4)+(y-3)(y-1)=0$
$\phantom{M\in\mathcal{C}} \Longleftrightarrow x^2-2x+4x-8+y^2-y-3y+3=0$
$\phantom{M\in\mathcal{C}} \Longleftrightarrow x^2+2x+y^2-4y-5=0$
Les deux équations obtenues sont équivalentes mais la seconde forme ne fait pas apparaître les coordonnées du centre et le rayon.
$x^2+2x+y^2-4y-5=0\Longleftrightarrow (x+1)^2-1+(y-2)^2-4-5=0 \Longleftrightarrow (x+1)^2+(y-2)^2=10 $
On peut contrôler le résultat avec GEOGEBRA.
Placer les points $A$ et $B$ puis le milieu $C$ de $[AB]$ et tracer le cercle (commande: cercle défini par son centre et un point) en pointant le centre $C$ puis $A$ ou $B$.
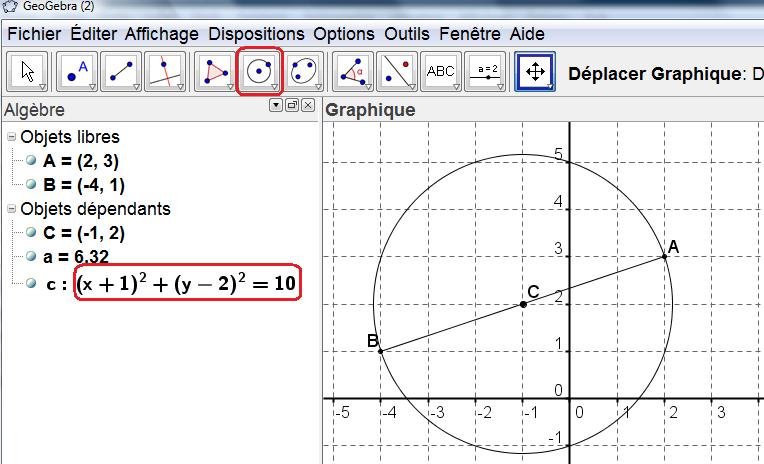
- $\mathcal{C}$ a pour diamètre $[AB]$ avec $A(2;1)$ et $B(3;-5)$
Coordonnées du milieu d'un segment
Dans un repère du plan, si on a $A(x_A;y_A)$ et $B(x_B;y_B)$ alors le milieu $I$ de $[AB]$ a pour coordonnées $I\left(\dfrac{x_A+x_B}{2};\dfrac{y_A+y_B}{2}\right)$Distance dans un repère
Dans un repère orthonormé du plan, on a $A(x_A;y_A)$ et $B(x_B;y_B)$,
$AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$
Si $\overrightarrow{u}(x;y)$ alors $||\overrightarrow{u}||=\sqrt{x^2+y^2}$On peut soit calculer les coordonnées du centre du cercle et son rayon $r=\dfrac{AB}{2}$
soit utiliser le fait que $M(x;y) \in \mathcal{C} \Longleftrightarrow \overrightarrow{AM}. \overrightarrow{BM}=0$Soit $C$ le milieu de $[AB]$
$\begin{cases} x_C =\dfrac{x_A+x_B}{2}=\dfrac{2+3}{2}=\dfrac{5}{2} \\ y_C =\dfrac{y_A+y_B}{2}=\dfrac{1-5}{2}=-2 \end{cases}$
donc $C(\dfrac{5}{2} ;-2)$ est le milieu de $[AB]$ donc le centre du cercle $\mathcal{C}$
$AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}=\sqrt{(1)^2+(-6)^2}=\sqrt{37}$
donc le cercle $\mathcal{C}$ a pour rayon $r=\dfrac{\sqrt{37}}{2}$
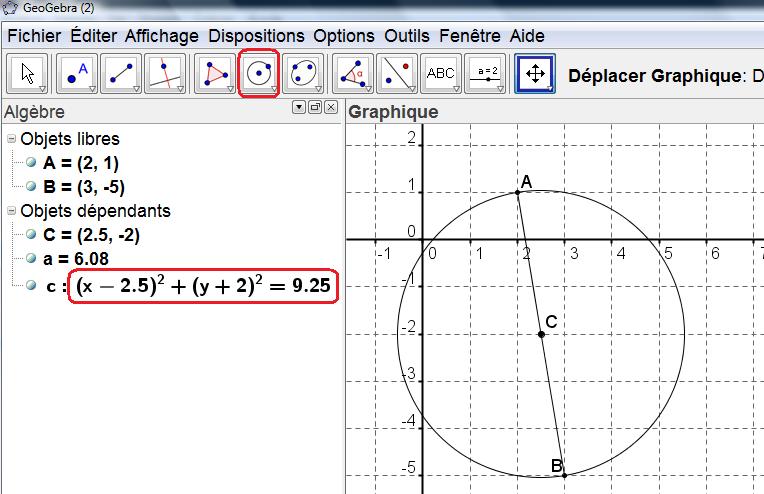
On a donc pour équation du cercle: $(x-\dfrac{5}{2})^2+(y-(-2))^2=\left(\dfrac{\sqrt{37}}{2} \right)^2$
On peut contrôler le résultat avec GEOGEBRA.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Fiche méthode
Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Équation d'un cercle
- déterminer une équation de cercle
- déterminer le centre et le rayon connaissant une équation du cercle
infos: | mn |
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
