La médiatrice $(d)$ de $[AB]$ passe par le milieu I de $[ AB]$ et est perpendiculaire à $(AB)$
$\begin{cases} x_{ \overrightarrow{AB}} = x_B - x_A = 3 - 0 = 3\\ y_{ \overrightarrow{AB}} = y_B - y_A = -3 - (-2) = -1 \end{cases}$
donc $ \overrightarrow{AB}(3;-1)$ est un vecteur directeur de $(AB)$ donc un vecteur normal à la droite $(d)$
Soit $I$ le milieu de $[AB]$ :
$\begin{cases} x_I =\dfrac{ x_A + x_B}{2}=\dfrac{3}{2} \\ y_I = \dfrac{ y_A + y_B}{2}=\dfrac{-3-2}{2}=\dfrac{-5}{2} \end{cases}$
donc $I(\dfrac{3}{2};\dfrac{-5}{2})$
Si $M(x; y)$ distinct de $I$ appartenant à $(d)$, $ \overrightarrow{IM}$ et $ \overrightarrow{AB}$ sont orthogonaux.
$\begin{cases} x_{ \overrightarrow{IM}} = x_M - x_I = x -\dfrac{3}{2}\\ y_{ \overrightarrow{IM}} = y_M - y_I = y+\dfrac{5}{2} \end{cases}$
donc $ \overrightarrow{IM}(x -\dfrac{3}{2}; y+\dfrac{5}{2})$
$ \overrightarrow{IM}. \overrightarrow{AB}=0$
$\Longleftrightarrow (x -\dfrac{3}{2})\times 3+(y+\dfrac{5}{2})\times (-1)=0$
$\Longleftrightarrow 3x -\dfrac{9}{2}-y-\dfrac{5}{2}=0$
$\Longleftrightarrow 3x-y-7=0$
$3x-y-7=0$ est une équation de $(d)$

La médiatrice $(d')$ de $[AC]$ passe par le milieu J de $[ AC]$ et est perpendiculaire à $(AC)$
$\begin{cases} x_{ \overrightarrow{AC}} = x_C - x_A = 8-0=8\\ y_{ \overrightarrow{AC}} = y_C - y_A = 2-(-2)=4 \end{cases}$
donc $ \overrightarrow{AC}(8;4)$ est un vecteur directeur de $(AC)$ donc un vecteur normal à la droite $(d')$
Soit $J$ le milieu de $[AC]$ :
$\begin{cases} x_J =\dfrac{ x_A + x_C}{2}=\dfrac{8+0}{2}=4 \\ y_J = \dfrac{ y_A + y_C}{2}=\dfrac{-2+2}{2}=0 \end{cases}$
donc $J(4;0)$
Soit $M(x; y)$ distinct de $J$ appartenant à $(d')$, $ \overrightarrow{JM}$ et $ \overrightarrow{AC}$ sont orthogonaux.
$\begin{cases} x_{ \overrightarrow{JM}} = x_M - x_J = x -4\\ y_{ \overrightarrow{JM}} = y_M - y_J = y \end{cases}$
donc $ \overrightarrow{JM}(x-4; y)$
$\overrightarrow{JM}. \overrightarrow{AC}=0$
$\Longleftrightarrow x_{ \overrightarrow{JM}}x_{ \overrightarrow{AC}}+y_{ \overrightarrow{JM}}y_{ \overrightarrow{AC}}=0$
$\Longleftrightarrow (x -4)\times 8+y\times 4=0$
$\Longleftrightarrow 8x+4y-32=0$
$\Longleftrightarrow 2x+y-8=0$
$2x+y-8=0$ est une équation de (d')

Le centre S du cercle circonscrit au triangle ABC est le point d'intersection des médiatrices $(d)$ et $(d')$
Il faut donc résoudre le système d'équations formé avec les équations de $(d)$ et $(d')$ :
$\phantom{\Longleftrightarrow}\begin{cases} 3x - y - 7 = 0 \\ 2x + y - 8 = 0 \end{cases}$
$\Longleftrightarrow\begin{cases} 3x- 7 = y \\ 2x +3x-7 - 8 = 0 \end{cases}$
$\Longleftrightarrow \begin{cases} 3x- 7 = y \\ 5x = 15 \end{cases}$
$\Longleftrightarrow \begin{cases} 3\times 3- 7 = y \\ x=3 \end{cases}$
$\Longleftrightarrow \begin{cases} 2 = y \\ x=3 \end{cases}$
donc $S(3;2)$
Calcul du rayon $r$ de ce cercle:
$r=SA=\sqrt{(x_A-x_S)^2+(y_A-y_S)^2}=\sqrt{(0-3)^2+(2-(-2))^2}=\sqrt{9+16}=5$
Le cercle circonscrit au triangle $ABC$ a donc pour centre $S(3;2)$ et rayon $r=5$
Une équation de ce cercle est donc:
$(x-x_S)^2+(y-y_S)^2=r^2$ soit ici $(x-3)^2+(y-2)^2=5^2$
$(x-3)^2+(y-2)^2=25$ est une équation du cercle circonscrit au triangle $ABC$

Soit $K$ le milieu de $[BC]$ :
$\begin{cases} x_K =\dfrac{ x_B + x_C}{2}=\dfrac{8+3}{2}=\dfrac{11}{2} \\ y_K =\dfrac{ y_B + y_C}{2}=\dfrac{-3+2}{2}=\dfrac{-1}{2} \\ \end{cases}$
donc $K(\dfrac{11}{2};\dfrac{-1}{2} )$
$\begin{cases} x_{ \overrightarrow{KS}} = x_S - x_K = 3-\dfrac{11}{2}=\dfrac{-5}{2}\\ y_{ \overrightarrow{KS}} = y_S - y_K = 2-\dfrac{-1}{2}=\dfrac{5}{2} \end{cases}$
donc $ \overrightarrow{KS}(\dfrac{-5}{2};\dfrac{5}{2})$
$\begin{cases} x_{ \overrightarrow{BC}} = x_C - x_B = 8-3=5\\ y_{ \overrightarrow{BC}} = y_C - y_B = 2-(-3)=5 \end{cases}$
donc $ \overrightarrow{BC}(5;5)$
$ \overrightarrow{KS}. \overrightarrow{BC}=x_{ \overrightarrow{KS}}x_{ \overrightarrow{BC}}+y_{ \overrightarrow{KS}}y_{ \overrightarrow{BC}}$
$\phantom{ \overrightarrow{KS}. \overrightarrow{BC}}=\dfrac{-5}{2}\times 5+\dfrac{5}{2}\times 5$
$\phantom{ \overrightarrow{KS}. \overrightarrow{BC}}=\dfrac{-25}{2}+\dfrac{25}{2}$
$\phantom{ \overrightarrow{KS}. \overrightarrow{BC}}=0$
donc $ \overrightarrow{KS}$ et $ \overrightarrow{BC}$ sont orthogonaux
donc $(KS) \perp (BC)$
Remarque:
La droite $(KS)$ est donc bien la médiatrice de $[BC]$
Les trois médiatrices sont concourantes en $S$.

Placer les points $A$, $B$ et $C$
Placer les points $I$ et $J$ (commande milieu) en pointant les sommets du triangle A et B puis A et C
puis tracer (commande droite perpendiculaire) les droites $(d)$ et $(d')$ puis vérifier que celles-ci sont sécantes en $S(3; 2)$
Tracer le cercle de centre S et rayon $SA$ par exemple.

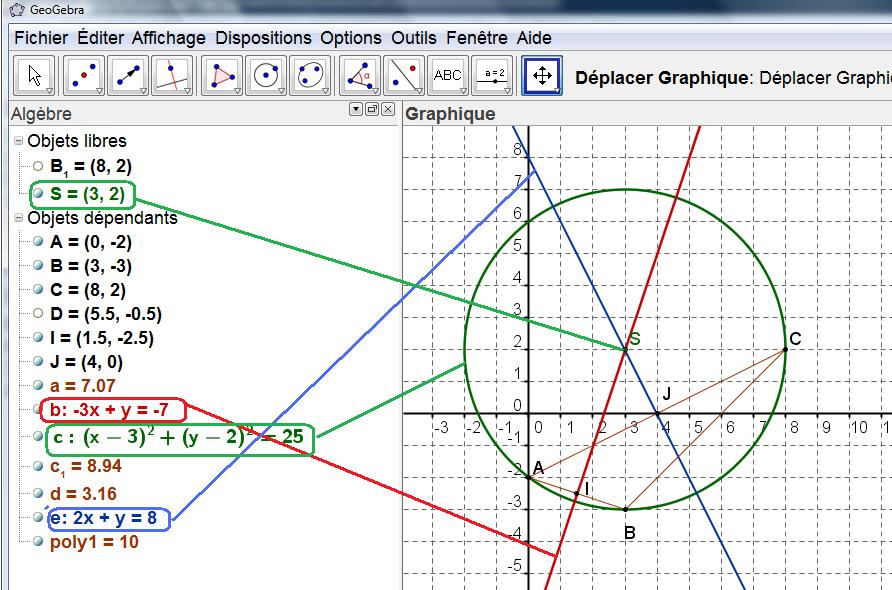
Ouvrir le fichier GEOGEBRA de la figure