MATHS-LYCEE.FR exercice corrigé chapitre Probabilités et variables aléatoires

Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.
*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)

PDF reservé aux abonnés

$A$ et $B$ sont deux événements et on donne:
La probabilité que l'événement $A$ soit réalisé est $0,3$
La probabilité que l'événement $B$ soit réalisé sachant que $A$ est réalisé est $0,6$
La probabilité que l'événement $B$ soit réalisé sachant que $A$ n'est pas réalisé est $0,2$

Compléter l'arbre ci-dessous:

Aide

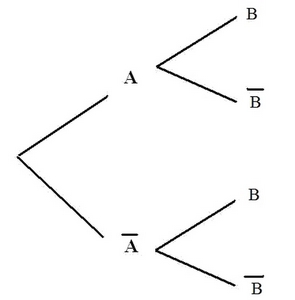Sur l'arbre pondéré, le coefficient de la première branche menant à l'événement A correspond à la probabilité $p(A)$
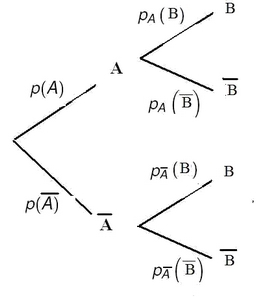
Sur l'arbre pondéré, le coefficient de la branche menant de l'événement A à l'événement B correspond à la probabilité $p_A(B)$
La somme des probabilités partant d'un noeud (point de départ des branches) est égale à 1

Solution

L'arbre se complète avec les probabilités suivantes:

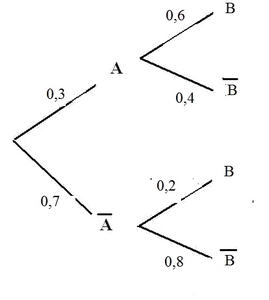
La probabilité que l'événement $A$ soit réalisé se note $p(A)=0,3$.
La probabilité que l'événement $B$ soit réalisé sachant que $A$ est réalisé se note $p_A(B)=0,6$.
La probabilité que l'événement $B$ soit réalisé sachant que $A$ n'est pas réalisé se note $p_{\overline{A}}(B)=0,2$.
On a donc:
Calculer $p(A \cap B)$.

Rappel de cours

Probabilité de l'événement $A\cap B$
Soient $A$ et $B$ deux événements avec $p(A)\neq 0$, on a
$p(A\cap B)=p(A)\times p_A(B)$

Aide

Il faut identifier le parcours sur l'arbre correspondant à $p(A\cap B)$ et effectuer le produit des coefficients

Solution

Arbre:

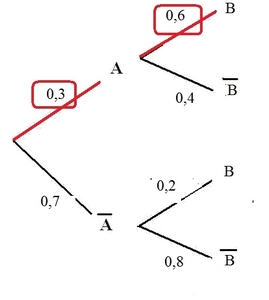
$p(A\cap B)=p(A)\times p_A(B)=0,3\times 0,6=0,18$
Calculer $p(A\cap \overline{B})$.

Aide

Il faut identifier le parcours sur l'arbre correspondant à $p(A\cap \overline{B}))$ et effectuer le produit des coefficients

Solution

$p(A\cap \overline{B})=p(A)\times p_A(\overline{B})=0,3\times 0,4=0,12$
Calculer $p(\overline{A}\cap B)$.

Solution

$p(\overline{A}\cap B)=p(\overline{A})\times p_{\overline{A}}(B)=0,7\times 0,2=0,14$