Exercice 1 (10 points)
On a testé les durées de vie de deux ampoules différentes.
1000 ampoules de type A ont été testées et 700 du type B.

- Calculer la durée de vie moyenne et l'écart type pour chaque type d'ampoule arrondis à l'heure près.(On ne demande pas le détail des calculs).
Commenter ces deux résultats.voir fiche méthode Statistiques et calculatrice.
Il faut saisir les durées dans la liste 1 puis les effectifs correspondants aux deux types d'ampoules dans les listes 2 et 3.
Paramétrer(CASIO) ensuite la calculatrice: 1VARX: LIST1 et 1VARF: LIST2
On obtient alors: $\overline{x_A}\simeq 949$ heures
et $\sigma_A\simeq 294$
Pour les ampoules de type B, on recommence en effectuant le paramétrage correspondant, à savoir: 1VARX: LIST1 et 1VARF: LIST3
On obtient alors: $\overline{x_B}\simeq 991$ heures
et $\sigma_B\simeq 344$
La durée de vie moyenne des ampoules de type B est supérieure de 46 heures à celles du groupe A mais on peut aussi dire que la durée de vie des ampoules de type B est plus "dispersée" par rapport à la moyenne. - Déterminer le pourcentage d'ampoules dont la durée de vie a un écart à la moyenne inférieur à l'écart type pour chacune des deux séries.
Proportion d'un ensemble
On considère une partie $A$ d'un ensemble $E$.
On appelle proportion de $A$ dans $E$ le quotient du nombre d'éléments de $A$ par le nombre d'éléments de $E$.
Remarque
En multipliant par $100$ le quotient obtenu, on trouve quel pourcentage d'éléments de $E$ représente $A$.On cherche le nombre d'ampoules de type A dont la durée de vie est comprise entre $[\overline{x_A}-\sigma_A;\overline{x_A}+\sigma_A]$ soit $[650;1240]$
Il y a 652 (100+110+130+107+105+100) ampoules répondant à ce critère soit $\dfrac{652}{1000}\times 100 =66,2$% des ampoules de type A.
On cherche le nombre d'ampoules de type B dont la durée de vie est comprise entre $[\overline{x_B}-\sigma_B;\overline{x_B}+\sigma_B]$ soit $[655;1243]$
Il y a 428 ampoules répondant à ce critère soit $\dfrac{428}{700}\times 100 \simeq 61,2$%des ampoules de type B.
- Compléter les deux lignes des effectifs cumulés croissants pour chaque type d'ampoule.
Déterminer la médiane, les premiers et troisième quartiles en justifiant les résultats.
Donner la signification du troisième quartile.Médiane
La médiane $M$ est la valeur du caractère telle que a 50% (la moitié) des valeurs soient inférieures ou égales à $M$ et l'autre moitié supérieures ou égale à $M$.
Exemple 1: Si l'effectif total est pair (par exemple 14 valeurs) alors la médiane est entre la 7ième et la 8ième valeur(valeurs classées dans l'ordre croissant)
Exemple 2: Si l'effectif total est impair (par exemple 15 valeurs) alors la médiane correspond à la 8ième valeur(valeurs classées dans l'ordre croissant)Quartiles
Le premier quartile $Q_1$ est la plus petite valeur du caractère telle que au moins 25% (un quart) des valeurs soient inférieures ou égales à $Q_1$.
Le troisième quartile $Q_3$ est la plus petite valeur du caractère telle que au moins 75% (trois quarts) des valeurs soient inférieures ou égales à $Q_3$.
L'intervalle $[Q_1;Q_3]$ est l'intervalle interquartile et $Q_3-Q_1$ est l'écart interquartile..

Les ampoules sont classées par ordre croissant de durée de vie.
La médiane $Med$ est la valeur du caractère telle que la moitié des ampoules ont une durée de vie inférieure ou égale à $Med$ et l'autre moitié ont une durée de vie supérieure ou égale à $Med$.
Il y 1000 ampoules (effectif pair) donc la médiane est comprise entre la durée de vie de la 500$^{\text{ième}}$ ampoule soit 900 heures et la durée de vie de de la 501$^{\text{ième}}$ ampoule soit 900 heures
donc $Med=900$ heures
25% de 1000 est égal à 250.
$Q_1$ est la plus petite durée de vie telle que au moins 250 ampoules A ont une durée de vie inférieure ou égale à $Q_1$
Le premier quartile correspond à la durée de vie de la 250$^{\text{ième}}$ ampoule soit $Q_1= 700 $ heures.
De même 75% de 1000 est égal à 750.
Le troisième quartile correspond à la durée de vie de la 750$^{\text{ième}}$ ampoule soit $Q_3= 1200 $ heures.
$Q_3=1250$ donc au moins 75% des ampoules ont une durée de vie inférieure ou égale à 1250 heures. - Le constructeur des ampoules de type A affirme que "plus de 75% de ses ampoules durent 700 heures ou plus".
Cette affirmation est-elle vraie?
La somme des effectifs correspondant à une durée de vie supérieure ou égale à 700 heures est de $1000-187=813$
soit $\dfrac{813}{1000}\times 100=81,3$% des ampoules donc l'affirmation est vraie.
Exercice 2 (10 points)
On donne dans le tableau suivant, les salaires annuels en milliers d'euros en Ile-de-France sur un groupe de 10 000 personnes:

- Calculer le salaire annuel moyen en Ile-de-France en indiquant les calculs effectués..
Moyenne
On considère la série de $N$ données $x_i$ ($i$ entier naturel compris entre $1$ et $N$) les valeurs du caractère et $n_i$ les effectifs correspondants.
$N=n_1+n_2+$.... est l'effectif total.
La moyenne de la série statistique est $\overline{x}=\dfrac{n_1x_1+n_2x_2+\text{.....}+n_px_p}{N}$.} Dans le cas d'une série regroupée en classe, on utilise le centre des classes pour faire le calcul de la moyenne.Attention, il faut utiliser le centre des classes pour faire le calculs de la moyenne et de l'écart type.
Rappel: Le centre de l'intervalle $[a;b]$ est $\dfrac{a+b}{2}$Moyenne avec les centres des classes:
$\overline{x}=\dfrac{9,5\times 50+10,5\times 50+13\times 50+17,5\times 256+22,5\times 244+27,5\times 125+35\times 125+45\times 100}{1000}\approx 24$
- Compléter la troisième ligne du tableau (effectifs cumulés croissants).
- Dresser le diagramme des effectifs cumulés croissants dans le repère ci-dessous (ne pas oublier la légende sur chacun des axes).
L'axe des abscisses correspond aux salaires et l'axe des ordonnées aux effectifs cumulés
Attention, l'effectif cumulé croissant 100 signifie qu'il y a 100 salaires inférieurs à 11 milliers d'euros donc il faut placer le point de coordonnées (11;100)Rappel de la signification des effectifs cumulés croissants:
L'effectif cumulé croissant 50 pour l'intervalle $[9;10[$ signifie que 50 personnes gagnent moins de 10 milliers d'euros annuellement et il faut donc placer le point de coordonnées (10;50)
De même, l'effectif cumulé croissant 100 pour l'intervalle $[10;11[$ signifie que 100 personnes gagnent moins de 11 milliers d'euros annuellement et il faut donc placer le point de coordonnées (11;100).....
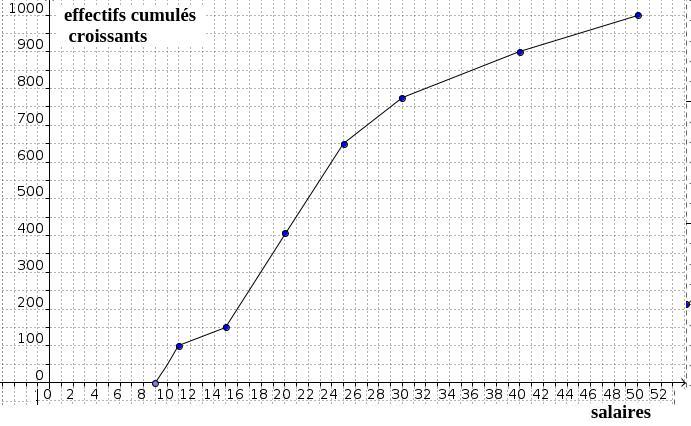
- A l'aide du graphique, déterminer le premier et neuvième décile, le premier et troisième quartile.
On laissera les tracés apparents sur le graphique et on notera les réponses sur la copie..
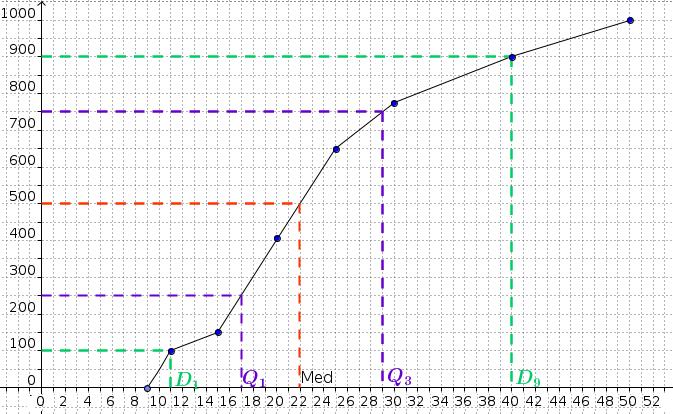
Graphiquement (tracés en couleur), on a:
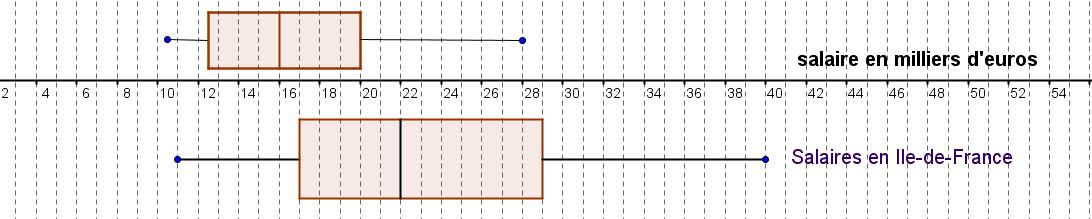
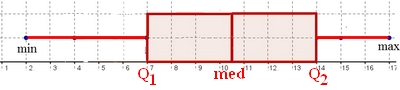
- Le diagramme en boîte ci-dessous correspond aux salaires annuels en milliers d'euros en province (pour les régions françaises hors Ile-de-France).
Compléter avec le diagramme en boîte pour les salaires de la région Ile-de-France.

Diagramme en boîte
Sur un axe gradué, on doit placer le minimum, $Q_1$, médiane, $Q_3$ et la valeur maximale.
- Donner l'écart inter-quartile pour chacune des deux séries de données.
En observant ces deux diagrammes, que peut-on dire des salaires en Ile de France et en province?0 L'écart interquartile est $Q_3-Q_1$Pour l'Ile-de-France: $Q_3-Q_1=29-17=12$ (milliers d'euros)
Pour la province, on lit sur le graphique $Q'_3-Q'_1=20-12,5=7,5$ (milliers d'euros)
On observe que les salaires sont beaucoup plus élevés en Ile-de-France mais aussi qu'ils sont beaucoup moins "homogènes" dans leur répartition.
En effet, l'écart inter-quartile (longueur de la "boîte" sur le diagramme) notamment est beaucoup plus important pour l'Ile-de-France.
Fiche méthode
Si ce devoir vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Médianes et quartiles avec une série discrète
- définitions
- méthode
- exemple
infos: | 10mn |
vidéos semblables
Pour compléter ce devoir, nous vous conseillons les vidéos suivantes pour préparer ce devoir.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
réf 473: Étude de séries discrètes
| 10-15mn |
réf 474: Étude complète d'une série discrète
| 8-10mn |
réf 475: Étude complète d'une série continue
| 10-15mn |
| 10-15mn |
réf 474: Étude complète d'une série discrète
| 8-10mn |
réf 475: Étude complète d'une série continue
| 10-15mn |