Exercice 1 (4 points)
Le plan est rapporté à un repère orthonormé qu'on pourra représenter et compléter au fur et à mesure de l'exercice (non exigé)
- Déterminer une équation cartésienne de la droite $\Delta$ perpendiculaire à la droite $d~~:~~2x+y+3=0$ passant par $A(-4;5)$.
Orthogonalité
Pour tous vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ non nuls, on a:
$\overrightarrow{u}.\overrightarrow{v}=0 \Longleftrightarrow \overrightarrow{u}$ et $\overrightarrow{v}$ sont orthogonaux.$\overrightarrow{n}(2;1)$ est un vecteur normal à la droite $d$ donc est un vecteur directeur de $\Delta$.
$\overrightarrow{n}(-b;a)$ donc $-b=2$ soit $b=-2$ et $a=1$
$\Delta$ admet une équation cartésienne de la forme $x-2y+c=0$
$A\in d \Longleftrightarrow x_A-2y_A+c=0 \Longleftrightarrow c=14$
- Déterminer une équation du cercle $\mathcal{C}$ de centre $I(-2;3)$ et de rayon 3.
$M(x;y)\in \mathcal{C} \Longleftrightarrow IM^2=3^2 \Longleftrightarrow (x-(-2))^2+(y-3)^2=9$
Exercice 2 (12 points)
Le plan est muni d'un repère orthonormal $(O;\overrightarrow{i};\overrightarrow{j})$. Soient $A(3;6)$ et $B(0;6)$.
On note $\mathcal{E}$ l'ensemble des points tels que $2MA^2+OM^2-MB^2=68$
On complètera la figure au fur et à mesure.
- Montrer que $\mathcal{E}$ est le cercle d'équation $x^2+y^2-6x-6y-7=0$ puis préciser son centre et son rayon.
Distance dans un repère
Dans un repère orthonormé du plan, on a $A(x_A;y_A)$ et $B(x_B;y_B)$,
$AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$
Si $\overrightarrow{u}(x;y)$ alors $||\overrightarrow{u}||=\sqrt{x^2+y^2}$Équation d'un cercle
Dans un repère orthonormé, le cercle de centre $C(x_C;y_C)$ et de rayon $r$ a pour équation $(x-x_C)^2+(y-y_C)^2=r^2$Exprimer les distances $MA^2$, $OM^2$ et $MB^2$ en fonction de $x$ et $y$ coordonnées de $M$ $(x-3)^2=x^2-6x+9$ et $(y-3)^2=y^2-6y+9$Soit $M(x;y)$ vérifiant $2MA^2+OM^2-MB^2=68$
$MA^2=(x-x_A)^2+(y-y_A)^2=(x-3)^2+(y-6)^2=x^2-6x+y^2-12y+45$
$MB^2=(x-x_B)^2+(y-y_B)^2=x^2+(y-6)^2=x^2+y^2-12y+36$
$OM^2=(x-x_O)^2+(y-y_O)^2=x^2+y^2$ (Le point $O$ a pour coordonnées $O(0;0)$)
$2MA^2+OM^2-MB^2=68 \Longleftrightarrow 2(x^2-6x+y^2-12y+45)+ x^2+y^2-(x^2+y^2-12y+36)=68$
$\phantom{2MA^2+OM^2-MB^2=68} \Longleftrightarrow 2x^2-12x+2y^2-24y+90+ x^2+y^2-x^2-y^2+12y-36=68$
$\phantom{2MA^2+OM^2-MB^2=68} \Longleftrightarrow 2x^2-12x+2y^2-12y+54=68$
$\phantom{2MA^2+OM^2-MB^2=68} \Longleftrightarrow 2x^2-12x+2y^2-12y-14=0$
$\phantom{2MA^2+OM^2-MB^2=68} \Longleftrightarrow x^2-6x+y^2-6y-7=0$ (on divise les deux membres par 2)
$x^2-6x+y^2-6y-7=0 \Longleftrightarrow (x-3)^2-9+(y-3)^2-9-9-7=0 \Longleftrightarrow (x-3)^2-9+(y-3)^2=25$
- Tracer le cercle $\mathcal{C}$ de centre $C(-2;\dfrac{1}{2})$ et de rayon $\dfrac{5}{2}$. En donner une équation sous forme développée.
Une équation de $\mathcal{C}$ est $(x-(-2))^2+(y-\dfrac{1}{2})^2=\left( \dfrac{5}{2}\right)^2 $
$ (x+2)^2+(y-\dfrac{1}{2})^2=\dfrac{25}{4} \Longleftrightarrow x^2+4x+4+y^2-y+\dfrac{1}{4}=\dfrac{25}{4}$
$\phantom{(x+2)^2+(y-\dfrac{1}{2})^2=\dfrac{25}{4}} \Longleftrightarrow x^2+4x+y^2-y+\dfrac{17}{4}=\dfrac{25}{4}$
$\phantom{(x+2)^2+(y-\dfrac{1}{2})^2=\dfrac{25}{4}} \Longleftrightarrow x^2+4x+4+y^2-y-\dfrac{8}{4}=0$ - Déterminer les coordonnées des points d'intersection de $\mathcal{E}$ et $\mathcal{C}$ ; on notera $I$ celui dont l'ordonnée est la plus grande, et $J$ l'autre point.
Il faut résoudre le système formé avec les équations des deux cercles sous forme développée.
Soutraire les deux lignes membre à membreIl faut résoudre le système formé avec les équations des deux cercles sous forme développée:
$\phantom{\Longleftrightarrow}\begin{cases} x^2-6x+y^2-6y-7=0 \\ x^2+4x+4+y^2-y-2=0 \end{cases}$
$\Longleftrightarrow \begin{cases} x^2-6x+y^2-6y-7=0 \\ -10x-5y-5=0~~~~~~ \text{Ligne 1-Ligne 2 ~soit }L_1-L_2 \end{cases}$
$\Longleftrightarrow \begin{cases} x^2-6x+y^2-6y-7=0 \\ -2x-y-1=0 ~~~~ \text{On divise les deux membres par 5} \end{cases}$
$\Longleftrightarrow \begin{cases} x^2-6x+(-2x-1)^2-6(-2x-1)-7=0 \\ -2x-1=y \end{cases}$
$\Longleftrightarrow \begin{cases} x^2-6x+4x^2+4x+1+12x+6-7=0 \\ -2x-1=y \end{cases}$
$\Longleftrightarrow \begin{cases} 5x^2+10x=0 \\ -2x-1=y \end{cases}$
$\Longleftrightarrow \begin{cases} 5x(x+2)=0 \\ -2x-1=y \end{cases}$
$\Longleftrightarrow \begin{cases} x=0 \\ -2x-1=y \end{cases}$ ou bien $ \begin{cases} x=-2 \\ -2x-1=y \end{cases}$
$\Longleftrightarrow \begin{cases} x=0 \\ -1=y \end{cases}~~~~~~~~$ou bien $\begin{cases} x=-2 \\ 3=y \end{cases} $
Il y a donc deux points d'intersection $I(-2;3)$ et $J(0;-1)$
-
- Déterminer une équation de la tangente à $\mathcal{E}$ en $J$ ; on note $T_{J}$ cette droite.
Soit $M(x;y)$ un point de la tangent, on a $\overrightarrow{JM}.\overrightarrow{JE}=0$$\begin{cases} x_{\overrightarrow{EJ}}=x_J-x_E=-3\\ y_{\overrightarrow{EJ}}=y_J-y_E=-4 \end{cases}$
donc $\overrightarrow{JE}(-3;-4)$ est un vecteur directeur de $(EJ)$
Soit $M(x;y)$ un point de $T_J$ tangente en $J$ à $\mathcal{E}$ $\begin{cases} x_{\overrightarrow{JM}}=x_M-x_J=x\\ y_{\overrightarrow{JM}}=y_M-y_J=y+1 \end{cases}$
donc $\overrightarrow{JM}(x;y+1)$
$T_J$ tangente en $J$ à $\mathcal{E}$ donc $T_J\perp (EJ)$
$M\in T_J \Longleftrightarrow \overrightarrow{JM}.\overrightarrow{JE}=0$
$\phantom{M\in T_J} \Longleftrightarrow x_{\overrightarrow{JM}}x_{\overrightarrow{JE}}+y_{\overrightarrow{JM}}y_{\overrightarrow{JE}}=0$
$\phantom{M\in T_J} \Longleftrightarrow x\times (-3)+(y+1)\times (-4)=0$
$\phantom{M\in T_J} \Longleftrightarrow -3x-4y-4=0$
$\phantom{M\in T_J} \Longleftrightarrow 3x+4y+4=0$
- Déterminer les coordonnées d'un vecteur directeur de la tangente à $\mathcal{C}$ en $J$ ; on note $T'_{J}$ cette droite.
$\begin{cases} x_{\overrightarrow{CJ}}=x_J-x_C=2\\ y_{\overrightarrow{CJ}}=y_J-y_C=-1-\dfrac{1}{2}=\dfrac{-3}{2} \end{cases}$
donc $\overrightarrow{CJ}(2;\dfrac{-3}{2})$ est vecteur directeur de $(CJ)$
$T'_J$ tangente en $J$ à $\mathcal{C}$ donc $T'_J\perp (CJ)$ et $J\in T'_J$
donc $\overrightarrow{w}(\dfrac{3}{2};2)$ vecteur normal à la droite $(CJ)$ est un vecteur directeur de $T'_J$
- Montrer que ces deux droites sont perpendiculaires (\textit{On dit que les cercles sont orthogonaux}).
Une équation de $T_J$ est $3x+4y+4=0$
donc $\overrightarrow{z}(-4;3)$ est un vecteur directeur de $T_J$
$\overrightarrow{w}.\overrightarrow{z}=\dfrac{3}{2}\times (-4)+2\times 3=-6+6=0$
donc $\overrightarrow{w}$ et $\overrightarrow{z}$ sont orthogonaux
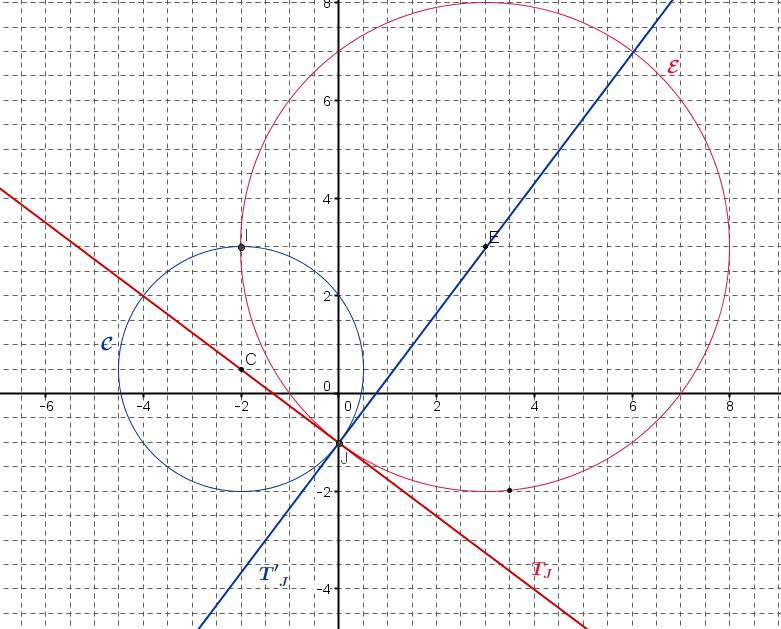
- Déterminer une équation de la tangente à $\mathcal{E}$ en $J$ ; on note $T_{J}$ cette droite.
Exercice 3 (4 points)
Dans le plan muni d'un repère orthonormé, on donne $A(2;6)$ et $B(-4;2)$.
Déterminer l'ensemble des points $M$ tels que $\overrightarrow{AM}.\overrightarrow{BM}=10$.
Développer et simplifier le calcul du produit scalaire
Soit $M(x;y)$ alors $\overrightarrow{AM}(x-2;y-6)$ et $\overrightarrow{BM}(x+4;y-2)$.
$\overrightarrow{AM}.\overrightarrow{BM}=10$
$\Longleftrightarrow (x-2)(x+4)+(y-6)(y-2)=10$
$\Longleftrightarrow x^2-2x+4x-8+y^2-6y-2y+12=10$
$\Longleftrightarrow x^2+2x+y^2-8y+4=10$
$\Longleftrightarrow (x+1)^2-1+(y-4)-16+4=10$
$\Longleftrightarrow (x+1)^2+(y-4)=23$
$\overrightarrow{AM}.\overrightarrow{BM}=10$
$\Longleftrightarrow (x-2)(x+4)+(y-6)(y-2)=10$
$\Longleftrightarrow x^2-2x+4x-8+y^2-6y-2y+12=10$
$\Longleftrightarrow x^2+2x+y^2-8y+4=10$
$\Longleftrightarrow (x+1)^2-1+(y-4)-16+4=10$
$\Longleftrightarrow (x+1)^2+(y-4)=23$
Fiche méthode
Si ce devoir vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Droites perpendiculaires
- déterminer si deux droites sont perpendiculaires
- déterminer une équation cartésienne d'une perpendiculaire
infos: | mn |
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.