Exercice 1 (8 points)
$ABCD$ est un tétraèdre régulier et les faces sont donc des triangles équilatéraux de côté 1. $I$ et $J$ sont les milieux respectifs des côtés $[AB]$ et $[BC]$.
- Calculer $\overrightarrow{DB}.\overrightarrow{IB}$.
Produit scalaire avec les projetés orthogonaux
Soit $A$, $B$ et $C$ trois points ($A$ et $B$ distincts) et $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$
Si $H$ est le projeté orthogonal de $C$ sur $(AB)$:
$\overrightarrow{u}.\overrightarrow{v}=AB\times AH$ si $\widehat{BAH}=0$ (soit $\widehat{BAC}$ aigu)
et $\overrightarrow{u}.\overrightarrow{v}=-AB\times AH$ si $\widehat{BAH}=\pi$ (soit $\widehat{BAC}$ obtus)On peut travailler dans le triangle équilatéral $ABD$ et donc dans le plan $(ABD)$Figure
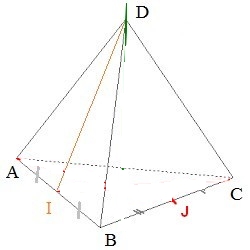
$I$ milieu de $[AB]$ et $ABD$ est équilatéral donc $(DI)$ est la médiane issue de $D$ dans $ABD$ et est confondue avec la hauteur issue de $D$ dans $ABD$
donc le projeté orthogonal de $D$ sur $(BI)$ est $I$.
$\overrightarrow{DB}.\overrightarrow{IB}=-\overrightarrow{BD}.(-\overrightarrow{BI})=\overrightarrow{BD}.\overrightarrow{BI}=BI^2=\dfrac{1}{4}$
- Calculer $\overrightarrow{DB}.\overrightarrow{BJ}$.
On peut travailler dans le triangle équilatéral $BCD$ et donc dans le plan $(BCD)$$J$ milieu de $[BC]$ et $BCD$ est équilatéral donc $(DJ)$ est la médiane issue de $D$ dans $BCD$ et est confondue avec la hauteur issue de $D$ dans $BCD$
donc le projeté orthogonal de $D$ sur $((BJ)$ est $J$.
$\overrightarrow{DB}.\overrightarrow{BJ}=-\overrightarrow{BD}.\overrightarrow{BJ}=-BJ^2=-\dfrac{1}{4}$
- En déduire $\overrightarrow{DB}.\overrightarrow{IJ}$.
Que peut-on en conclure pour les droites $(DB)$ et $(IJ)$?On peut décomposer $\overrightarrow{IJ}=\overrightarrow{IB}+\overrightarrow{BJ}$$\overrightarrow{DB}.\overrightarrow{IJ}=\overrightarrow{DB}.(\overrightarrow{IB}+\overrightarrow{BJ})$
$\phantom{\overrightarrow{DB}.\overrightarrow{IJ}}=\overrightarrow{DB}.\overrightarrow{IB}+\overrightarrow{DB}.\overrightarrow{BJ}$
$\phantom{\overrightarrow{DB}.\overrightarrow{IJ}}=\dfrac{1}{4}-\dfrac{1}{4}$ d'après les questions précédentes
$\phantom{\overrightarrow{DB}.\overrightarrow{IJ}}=0$
- Construire la droite d'intersection des plans $((DIC)$ et $(ADJ)$.
Il faut trouver deux points communs aux deux plans pour tracer la droite d'intesrsection$D$ appartient aux plans $(DIC)$ et $(DAJ)$.
Les droites $(AJ)$ et $(CI)$ sont coplanaires et non parallèles (plan $(ABC)$) donc sécantes.
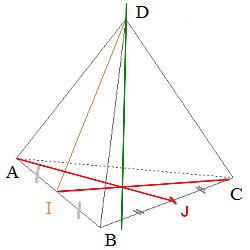
La droite d'intersection des deux plans est tracée en vert.Exercice 2 (12 points)$ABCDEFGH$ est un cube et $I$, $J$, $K$ et $L$ sont les milieux respectifs des côtés $[AB]$, $[AE]$, $[GC]$ et $[HG]$.
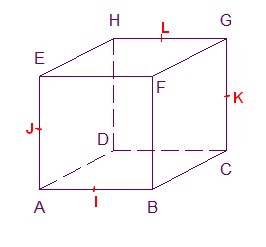
- Montrer que la droite $(BC)$ est orthogonale au plan $(ABF)$.
Orthogonalité et produit scalaire
Pour tous vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$, on a:
$\overrightarrow{u}.\overrightarrow{v}=0 \Longleftrightarrow \overrightarrow{u}=\overrightarrow{0}$ ou $\overrightarrow{v}=\overrightarrow{0}$ ou $\overrightarrow{u}$ et $\overrightarrow{v}$ sont orthogonaux.On peut utiliser les droites $(AB)$ et $(BF)$$ABCD$ est un carré donc $(AB)$ est orthogonale à $(BC)$.
$BCGF$ est un carré donc $(BF)$ est orthogonale à $(BC)$
donc $(BC)$ est orthogonale à deux droites $(AB)$ et $(BF)$ sécantes du plan $(ABF)$
- En déduire que $(IJ)$ est orthogonale à $(BC)$.
On utilise la question 1 et la droite $(IJ)$ est contenue dans le plan $(ABC)$$I\in [AB]$ et $J\in [AE]$ donc $(IJ)$ est contenue dans le plan $(ABF)$ (ou $(ABE)$)
or $(BC)$ est orthogonale au plan $(ABF)$ donc à toute droite du plan $(ABF)$
- Quelle est la nature du quadrilatère $IJLK$?
Il faut montrer que les vecteurs $\overrightarrow{IJ}$ et $\overrightarrow{LK}$ sont égaux.
On peut décomposer $\overrightarrow{IJ}=\overrightarrow{IA}+\overrightarrow{AJ}$ et $\overrightarrow{LK}=\overrightarrow{KG}+\overrightarrow{GH}$Les faces étant des carrés, on a:
$\overrightarrow{BA}=\overrightarrow{CD}=\overrightarrow{GH}$
$\overrightarrow{AE}=\overrightarrow{DH}=\overrightarrow{CG}$
$\overrightarrow{IJ}=\overrightarrow{IA}+\overrightarrow{AJ}$
$\phantom{\overrightarrow{IJ}}=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{AE}$
$\phantom{\overrightarrow{IJ}}=\dfrac{1}{2}\overrightarrow{GH}+\dfrac{1}{2}\overrightarrow{CG}$
$\phantom{\overrightarrow{IJ}}=\overrightarrow{GL}+\overrightarrow{KG}$
$\phantom{\overrightarrow{IJ}}=\overrightarrow{KL}$
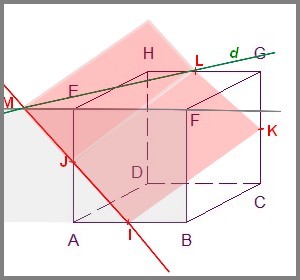
- Construire la droite $d$ intersection des plans $(IJK)$ et $(EFG)$.
Il faut construire deux points de $d$ en utilisant des droites coplanaires contenues dans les deux plans$IJKL$ est un parallélogramme donc les points $I$, $J$, $K$ et $L$ sont coplanaires
donc $L$ appartient aux plans $(IJK)$ et $(EFG)$ (car $L\in [HG]$)
Les droites $(IJ)$ et $(EF)$ sont coplanaires (contenues dans le plan $(ABF)$)
et non parallèles donc sécantes en $M$ avec $M$ appartenant aux plans $(IJK)$ et $(EFG)$
donc la droite $(ML)$ est l'intersection des plans $(IJK)$ et $(EFG)$.
Fiche méthode
Si ce devoir vous pose problème, nous vous conseillons de consulter la fiche méthhode.Intersections de plans et droites
- méthode de construction de l'intersection de deux plans
infos: | 15-20mn |exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.réf 1342: Produit scalaire dans un cube
| 8-12mn |
réf 1347: Intersections dans un tétraèdre
| 10-12mn |
- Quelle est la nature du quadrilatère $IJLK$?
- Construire la droite d'intersection des plans $((DIC)$ et $(ADJ)$.