Exercice 1 (7 points)
- Résoudre dans $\mathbb{R}$ l'inéquation $e^{-2x-1}>1$
Égalité et inégalités avec exponentielle
Pour tous réels $a$ et $b$, on a:
$e^a=e^b\Longleftrightarrow a=b$
$e^a < e^b\Longleftrightarrow a < b$
Remplacer 1 par $e^0$Rappel: $e^0=1$
$e^{-2x-1}>1 \Longleftrightarrow e^{-2x-1}>e^0$
$\phantom{e^{-2x-1}>1} \Longleftrightarrow -2x-1>0$
$\phantom{e^{-2x-1}>1}\Longleftrightarrow -2x>1$
$\phantom{e^{-2x-1}>1}\Longleftrightarrow x<\dfrac{1}{-2}$ l'inégalité change de sens car on divise par $-2$ (négatif)
- Résoudre dans $\mathbb{R}$ l'équation $e^{x^2}=e^{-3x+2}$
Racines
Les racines de $p(x)=ax^2+bx+c$ avec$a\neq 0$ sont les valeurs de $x$ annulant $P$
c'est à dire telles que $P(x)=0$.
$\Delta=b^2-4ac$
Si $\Delta>0$ donc il y a deux racine $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}$ et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}$
Si $\Delta=0$ il y a une racine (double) $x_1=\dfrac{-b}{2a}$
Si $\Delta<0$ il n'y a aucune racine
Remarque: Graphiquement, les racines sont les abscisses des points d'intersection de la parabole et de l'axe des abscisses.$e^{x^2}=e^{-3x+2} \Longleftrightarrow x^2=-3x+2$
$\phantom{e^{x^2}=e^{-3x+2}} \Longleftrightarrow x^2+3x-2=0$
$\Delta=b^2-4ac=9-4\times (1)\times (-2)=17$
$\Delta>0$ donc il y a deux solutions:
$x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-3-\sqrt{17}}{2}$
et $x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-3+\sqrt{17}}{2}$
- Résoudre dans $\mathbb{R}$ l'équation $-2X^2-3X+5=0$
En déduire les solutions de l'équation $-2e^{2x}-3e^x+5=0$Poser $X=e^x$ et on a alors $e^{2x}=(e^x)^2=X^2$$\Delta=b^2-4ac=(-3)^2-4\times (-2)\times 5=49$
$\Delta>0$ donc il y a deux solutions:
$x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{3-7}{-4}=1$
et $x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{3+7}{-4}=\dfrac{10}{-4}=\dfrac{-5}{2}$
On pose $X=e^{x}$
et on a alors $e^{2x}=e^{x^2}=X^2$
Il faut donc résoudre l'équation $-2X^2-3X+5=0$
d'après la question précédente, on a:
$X=1$ ou bien $X=\dfrac{-5}{2}$
Or $X=e^x$ donc il faut résoudre:
$X=1$ soit $e^x=1$
$e^x=1 \Longleftrightarrow e^x=e^0 \Longleftrightarrow x=0$
et $e^x=\dfrac{-5}{2}$
Pour tout réel $x$, on a $e^x>0$
donc l'équation $e^x=\dfrac{-5}{2}$ n'admet aucune solution
Exercice 2 (13 points)
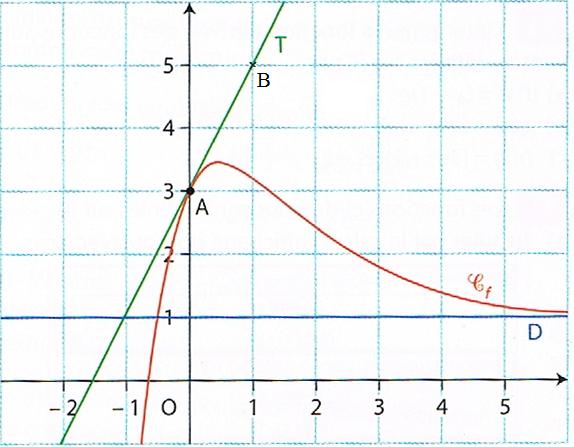
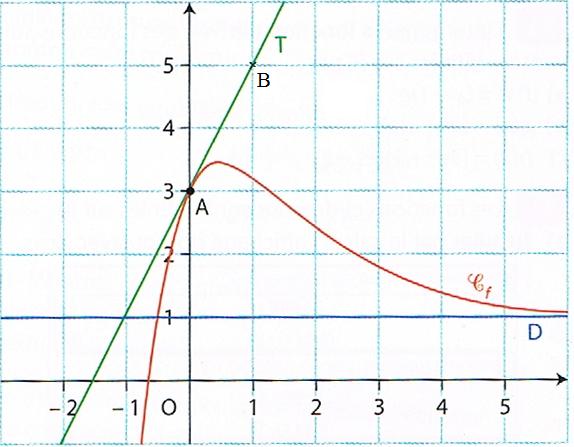
Dans le plan muni d'un repère orthogonal, la courbe $\mathcal{C}$ ci-dessous représente une fonction $f$ définie sur l'ensemble $\mathbb{R}$ des nombres réels.
La tangente $\mathcal{T}$ à la courbe $\mathcal{C}$ au point A$(0~;-4)$ passe par le point B$(2~;~- 6)$.
Partie A
On désigne par $f~'$ la fonction dérivée de $f$.
-
- Donner la valeur de $f(0)$.
Le point $A(0;-4) \in \mathcal{C}$
- Justifier que : $f~'(0) = - 1$.
Équation de la tangente au point d'abscisse $a$
$f$ est une fonction définie et dérivable en $x=a$.
La tangente à $C_f$ en $a$ a pour coefficient directeur $f'(a)$
et pour équation réduite $ y=f'(a)(x-a)+f(a)$}Il faut déterminer le coefficient directeur de la tangente au point d'abscisse 0$f~'(0)$ est le coefficient directeur de la tangente $\mathcal{T}$ à la courbe $\mathcal{C}$ au point $A(0;-4)$ d'abscisse 0 et T passe par $B(-4;0)$
donc $f~'(0)=\dfrac{y_B-y_A}{x_B-x_A}=\dfrac{0-(-4)}{-4-0}=-1$
- Donner la valeur de $f(0)$.
-
- On admet qu'il existe deux réels $a$ et $b$ tels que, pour tout réel $x$, $f(x) = (x + a)\text{e}^{bx}$.
Vérifier que pour tout réel $x$, $f~'(x) = (bx + ab + 1)\text{e}^{bx}$.On pose $u(x)=x+a $ et $v(x)=e^{bx} $On pose $u(x)=x+a $ et $v(x)=e^{bx} $
et on a $u'(x)= 1 $ et $v'(x)=be^{bx} $
$f~'(x)=u'(x)v(x)+u(x)v'(x)$
$\phantom{f~'(x)}=( 1)( e^{bx} )+( x+a ) ( be^{bx} )$
$\phantom{f~'(x)}= e^{bx}+ xbe^{bx} + abe^{bx} $
$\phantom{f~'(x)}= e^{bx}(bx+ab+1) $ (on factorise par $e^{bx}$)
- Utiliser les résultats précédents pour déterminer les valeurs exactes des réels $a$ et $b$.
Ecrire deux équations d'inconnues $a$ et $b$ sachant que $f(0)=-4$ et que $f~'(0)=-1$$f(0)=(0 + a)e^{b\times 0}=-4 \Longleftrightarrow ae^0=-4$ (rappel $e^0=1$) $\phantom{f(0)=(0 + a)\text{e}^{b\times 0}=-4}\Longleftrightarrow a=-4$
$a=-4$ donc $f~'(x)=e^{bx}(bx-4b+1)$
$f~'(0)= e^{b\times 0}(b\times 0-4b+1)=-1 \Longleftrightarrow -4b+1=-1$ (rappel $e^0=1$)
$\phantom{f~'(0)= e^{b\times 0}(b\times 0-4b+1)=-1}\Longleftrightarrow -4b=-2$
$\phantom{f~'(0)= e^{b\times 0}(b\times 0-4b+1)=-1}\Longleftrightarrow b=\dfrac{-2}{-4}$
$\phantom{f~'(0)= e^{b\times 0}(b\times 0-4b+1)=-1}\Longleftrightarrow b=\dfrac{1}{2}$
$\phantom{f~'(0)= e^{b\times 0}(b\times 0-4b+1)=-1} \Longleftrightarrow -4b=\dfrac{-1}{e}-1$
- On admet qu'il existe deux réels $a$ et $b$ tels que, pour tout réel $x$, $f(x) = (x + a)\text{e}^{bx}$.
On considère maintenant la fonction $f$ définie pour tout réel $x$ par $f(x) = (x - 4)e^{0,5x}$.
- Donner l'expression de $f~'(x)$ pour tout réel $x$ ; en déduire le sens de variation de la fonction $f$ sur l'ensemble des réels $\mathbb{R}$.
Signe de exp(x)
Pour tout réel $x$ on a $e^x>0$Utiliser l'expression de $f~'(x)$ et $a=-4$ et $b=0,5$D'après les questions 2a. et 2b., on a $f~'(x)= e^{bx}(bx+ab+1) $ avec $a=-4$ et $b=0,5$
donc $f~'(x)=e^{0,5x}(0,5x-2+1)=e^{0,5x}(0,5x-1)$
$e^{0,5x}>0$ donc $f~'(x)$ est du signe de $0,5x-1$
$0,5x-1>0 \Longleftrightarrow 0,5x>1 \Longleftrightarrow x>\dfrac{1}{0,5} \Longleftrightarrow x>2$
donc $f~'(x)>0$ sur $2;+\infty[$ et $f~'(x)<0$ sur $]-\infty;2[$
- On considère la fonction $g$ définie pour tout réel $x$ par $g(x)=f(x)+x+4$. On admet que la fonction $g$ est strictement croissante sur $\mathbb{R}$.
- Calculer $g(0)$ et en déduire le signe de $g(x)$
$g(0)=f(0)+0+4=-4+4=0$
$g$ est strictement croissante et continue sur $\mathbb{R}$
et $g(0)=0$ donc $g(x)>0$ pour $x>0$
Avec le tableau de variation de $g$ on a:
- Déterminer l'équation réduite de la tangente $T$ à la courbe $\mathcal{C}$ au point d'abscisse $0$ par le calcul.
Équation de la tangente au point d'abscisse $a$
$f$ est une fonction définie et dérivable en $x=a$.
La tangente à $C_f$ en $a$ a pour coefficient directeur $f'(a)$
et pour équation réduite $ y=f'(a)(x-a)+f(a)$}Calculer $f(0)$ et $f'(0)$$f(0) = (0 - 4)e^{0,5\times 0}=-4$ (rappel: $e^0=1$)
$f~'(0)=e^{0,5\times 0}(0,5\times 0-1)=-1$
$T$: $y=f'(0)(x-0)+f(0)=-1x-4$
- Déterminer la position de la courbe $\mathcal{C}$ par rapport à sa tangente $\mathcal{T}$
Il faut étudier le signe de $f(x)-(-x+4)$
Utiliser le résultat concernant le signe de g(x)La tangente $\mathcal{T}$ a pour équation réduite $y=-x-4$
et $f(x)-(-x-4)=f(x)+x+4=g(x)$
donc d'après la question précédente, on a:
$f(x)-(-x-4)<0$ sur $]-\infty;0[$
et $f(x)-(-x-4)>0$ sur $]0;+\infty[$
$\mathcal{C}$ est au-dessus de $\mathcal{T}$ pour $x > 0$
et $\mathcal{C}$ est en-dessous de $\mathcal{T}$ pour $x < 0$
donc la tangente $T$ au point d'abscisse $0$ coupe la courbe $\mathcal{C}$ et on dit que le point de la courbe d'abscisse $0$ est un point d'inflexion.
- Calculer $g(0)$ et en déduire le signe de $g(x)$
vidéos semblables
Pour compléter ce devoir, nous vous conseillons les vidéos suivantes pour préparer ce devoir.
réf 1020: Dérivées avec exponentielle
| 3mnmn |
réf 1022: Dérivées avec la fonction exponentielle
| 3mn40smn |
| 3mnmn |
réf 1022: Dérivées avec la fonction exponentielle
| 3mn40smn |
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
réf 986: Simplifications avec exp et utilisation des propriétés algébriques
| 4-6mn |
réf 990: Dérivée de base avec exp et formules de dérivation
| 6-10mn |
réf 1000: Équations avec exponentielle (niv2)
| 5-8mn |
réf 1001: Inéquations avec exponentielle
| 4-6mn |
réf :
| mn | validé| vu le 01/01/1970
| 4-6mn |
réf 990: Dérivée de base avec exp et formules de dérivation
| 6-10mn |
réf 1000: Équations avec exponentielle (niv2)
| 5-8mn |
réf 1001: Inéquations avec exponentielle
| 4-6mn |
réf :
| mn | validé| vu le 01/01/1970