Exercice 1 (8 points)
L'espace est rapporté au repère orthonormal .
On considère le plan $\mathcal{P}$ d'équation $2x + y - 2z + 4 = 0$ et les points $A$ de coordonnées $(3 ; 2 ; 6)$, B de coordonnées $(1 ; 2 ; 4)$, et $C$ de coordonnées $(4;-2;5)$.
- Vérifier que les points A, B et C définissent un plan.
Coordonnées d'un vecteur dans l'espace
L'espace est muni d'un repère quelconque.
Soit $A(x_A;y_A;z_A)$ et $B(x_B;y_B;z_B)$
$\overrightarrow{AB}\begin{pmatrix} x_B-x_A\\ y_B-y_A\\ z_B-z_A \end{pmatrix} $vecteurs coplanaires
Trois vecteurs $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ non nuls sont coplanaires si les points $A$, $B$, $C$ et $D$ définis par $\overrightarrow{AB}=\overrightarrow{u}$, $\overrightarrow{AC}=\overrightarrow{v}$ et $\overrightarrow{AD} =\overrightarrow{w}$ sont dans un même plan.
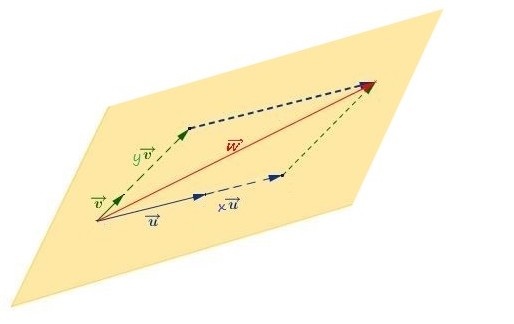 Il faut vérifier que les points $A$, $B$ et $C$ ne sont pas alignés donc que les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ ne sont pas colinéaires$\begin{cases} x_{\overrightarrow{AB}}=x_B-x_A=1-3=-2\\ y_{\overrightarrow{AB}}=y_B-y_A=2-2=0\\ z_{\overrightarrow{AB}}=z_B-z_A=4-6=-2 \end{cases}$
Il faut vérifier que les points $A$, $B$ et $C$ ne sont pas alignés donc que les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ ne sont pas colinéaires$\begin{cases} x_{\overrightarrow{AB}}=x_B-x_A=1-3=-2\\ y_{\overrightarrow{AB}}=y_B-y_A=2-2=0\\ z_{\overrightarrow{AB}}=z_B-z_A=4-6=-2 \end{cases}$
donc $\overrightarrow{AB}\begin{pmatrix} -2\\ 0\\ -2 \end{pmatrix} $
$\begin{cases} x_{\overrightarrow{AC}}=x_C-x_A=4-3=1\\ y_{\overrightarrow{AC}}=y_C-y_A=-2-2=-4\\ z_{\overrightarrow{AC}}=z_C-z_A=5-6=-1 \end{cases}$
donc $\overrightarrow{AC}\begin{pmatrix} 1\\ -4\\ -1 \end{pmatrix} $
$x_{\overrightarrow{AB}}=x_{\overrightarrow{AC}}$
mais $y_{\overrightarrow{AB}}\neq y_{\overrightarrow{AC}}$
donc il n'existe pas de réel $k$ tel que $k\overrightarrow{AB}=\overrightarrow{AC}$
donc les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ ne sont pas colinéaires
donc les points $A$, $B$ et $C$ ne sont pas alignés
- Vérifier que ce plan est le plan $\mathcal{P}$.
Il faut vérifier que les points $A$, $B$ et $C$ appartiennent à $\mathcal{P}$$2x_A + y_A - 2z_A + 4 = 6+2-12+4= 0$ donc $A\in \mathcal{P}$
$2x_B + y_B - 2z_B + 4 = 2+2-8+4= 0$ donc $B\in \mathcal{P}$
$2x_C + y_C - 2z_C + 4 =8-2-10+4=0$ donc $C\in \mathcal{P}$
donc $P$ et $(ABC)$ sont deux plans confondus
- Montrer que le triangle $ABC$ est rectangle.
Produit scalaire dans un repère orthonormé de l'espace
Dans un repère orthonormé de l'espace, on a les vecteurs $\overrightarrow{u}\begin{pmatrix} x\\ y\\ z \end{pmatrix}$ et $\overrightarrow{v}\begin{pmatrix} x'\\ y'\\ z' \end{pmatrix}$.
$\overrightarrow{u}.\overrightarrow{v}=xx'+yy'+zz'$Orthogonalité et produit scalaire
Pour tous vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$, on a:
$\overrightarrow{u}.\overrightarrow{v}=0 \Longleftrightarrow \overrightarrow{u}=\overrightarrow{0}$ ou $\overrightarrow{v}=\overrightarrow{0}$ ou $\overrightarrow{u}$ et $\overrightarrow{v}$ sont orthogonaux.Il faut vérifier si les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ sont orthogonaux.$\overrightarrow{AB}\begin{pmatrix} -2\\ 0\\ -2 \end{pmatrix} $ et $\overrightarrow{AC}\begin{pmatrix} 1\\ -4\\ -1 \end{pmatrix} $
donc $\overrightarrow{AB}.\overrightarrow{AC}=-2\times 1+0\times (-4)+(-2)\times (-1)=-2+2=0$
donc les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ sont orthogonaux
- Déterminer une représentation paramétrique de paramétriques de la droite $\Delta$ passant par l'origine du repère et perpendiculaire
au plan $\mathcal{P}$.
Vecteur normal à un plan-équation cartésienne d'un plan
Dans l'espace muni d'un repère othonormé, $P$ est un plan de l'espace, un vecteur $\overrightarrow{n}$ normal à $P$ est un vecteur directeur d'une droite orthogonale à $P$.
Le vecteur $\overrightarrow{n}$ est un vecteur normal au plan $P$ passant par $A$ et $P$ est l'ensemble des points $M(x;y;z)$ vérifiant $\overrightarrow{AM}.\overrightarrow{n}=0$.
$ax+by+cz+d=0$ est une équation cartésienne de $P$ de vecteur normal $\overrightarrow{n}\begin{pmatrix} a\\ b\\ c \end{pmatrix}$Un vecteur normal au plan $\mathcal{P}$ est un vecteur directeur de $\Delta$$\mathcal{P}$ a pour équation $2x + y - 2z + 4 = 0$
donc $\overrightarrow{n}\begin{pmatrix} 2\\ 1\\ -2 \end{pmatrix} $ est un vecteur directeur de $\Delta$
Si $M(x;y;z)$ appartient à $\Delta$, on a alors;
$\begin{cases} x=x_O+tx_{\overrightarrow{n}}=2t\\ y=y_O+ty_{\overrightarrow{n}}=t\\ z=z_O+tz_{\overrightarrow{n}}=-2t\end{cases}$
- Calculer les coordonnées du point d'intersection $H$ de $\Delta$ et de $(ABC)$
Il faut écrire une équation d'inconnue $t$ en remplaçant dans l'équation de $(ABC)$ les expressions de $x$, $y$ et $z$ données avec la représentation paramétrique de $\Delta$.Un point $M(x;y;z)$ appartient à $(ABC)$ si ses coordonnées vérifient $2x-y+3z+1=0$
La représentation paramétrique de $\Delta$ est $\begin{cases} x=2t\\ y=t\\ z=-2t \end{cases}$ et en remplaçant $x$, $y$ et $z$ dans l'équation de $(ABC)$ obtenue, on a:
$2\times 2t + t-2\times (-2t) + 4 = 0 \Longleftrightarrow 4t+t+4t+4=0$
$\phantom{2\times 2t + t-2\times (-2t) + 4 = 0} \Longleftrightarrow 9t+4=0$
$\phantom{2\times 2t + t-2\times (-2t) + 4 = 0} \Longleftrightarrow t=\dfrac{-4}{9}$
En remplaçant $t=\dfrac{-4}{9}$ dans la représentation paramétrique de $\Delta$, on obtient:
$\begin{cases} x_H=2t=2\times \dfrac{-4}{9}=\dfrac{-8}{9}\\ y_H=t=\dfrac{-4}{9}\\ z_H=-2t=\dfrac{8}{9} \end{cases}$
- En déduire le volume du tétraèdre $OABC$.
Distance dans l'espace
Si le repère de l'espace est orthonormé, la distance $AB$ est: $AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2+(z_B-z_A)^2}$Il faut calculer les distances $AB$, $AC$ et $OH$
Rappel: $V=\dfrac{\text{Aire de la base}\times \text{hauteur}{3}$$H$ est le point d'intersection de la droite $\Delta$ et du plan $(ABC)$ donc $(OK)$ est la hauteur issue de $O$ dans le tétraèdre $OABC$ ($H$ projeté orthogonal de $O$ sur $(ABC)$) donc $OH$ est la hauteur du tétraèdre.
$AB=\sqrt{x_{\overrightarrow{AB}}^2+y_{\overrightarrow{AB}}^2+z_{\overrightarrow{AB}}^2}=\sqrt{(-2)^2+0^2+(-2)^2}=\sqrt{8}=2\sqrt{2}$
$AC=\sqrt{x_{\overrightarrow{AC}}^2+y_{\overrightarrow{AC}}^2+z_{\overrightarrow{AC}}^2}=\sqrt{1^2+(-4)^2+(-1)^2}=\sqrt{18}=3\sqrt{2}$
$\mathcal{A}=\dfrac{2\sqrt{2}\times 3\sqrt{2}}{2}=\dfrac{12}{2}=6$
$OK=\sqrt{\left(\dfrac{-8}{9}\right)^2+\left(\dfrac{-4}{9}\right)^2+\left(\dfrac{8}{9}\right)^2}$
$=\sqrt{\dfrac{144}{81}}$
$=\sqrt{\dfrac{16}{9}}$
$=\dfrac{4}{3}$
$\mathcal{V}=\dfrac{6\times \dfrac{4}{3}}{3}=\dfrac{12}{3}=4$
Exercice 2 (12 points)
L'espace est rapporté au repère orthonormal $(O;I;J;K)$ .
On considère les points $A(0 ; 2 ; 0)$, $B(0 ; 0 ; 6)$, $C(4;0;0)$, $D(0;4;0)$ et $E(0;0;4)$.
- Vérifier que le vecteur $\overrightarrow{n}\begin{pmatrix}
1\\
1\\
1
\end{pmatrix}$ est un vecteur normal au plan $(CDE)$.
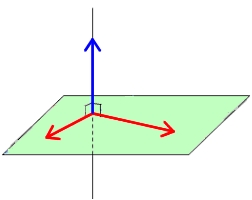
droite et plan orthogonaux
Une droite $(d)$ est orthogonale à un plan si et seulement si un vecteur directeur de $(d)$ est orthogonal à deux vecteurs directeurs de du plan.
Produit scalaire dans un repère orthonormé de l'espace
Dans un repère orthonormé de l'espace, on a les vecteurs $\overrightarrow{u}\begin{pmatrix} x\\ y\\ z \end{pmatrix}$ et $\overrightarrow{v}\begin{pmatrix} x'\\ y'\\ z' \end{pmatrix}$.
$\overrightarrow{u}.\overrightarrow{v}=xx'+yy'+zz'$Il faut vérifier que le vecteur $\overrightarrow{n}$ est orthogonal aux vecteurs $\overrightarrow{CD}$ et $\overrightarrow{CE}$$\overrightarrow{CD}\begin{pmatrix} -4\\ 4\\ 0 \end{pmatrix}$ et $\overrightarrow{CE}\begin{pmatrix} -4\\ 0\\ 4 \end{pmatrix}$
$\overrightarrow{n}.\overrightarrow{CD}=1\times (-4)+1\times 4+1\times 0=4-4=0$
et $\overrightarrow{n}.\overrightarrow{CE}=1\times (-4)+1\times 0+1\times 4=4-4=0$
donc le vecteur $\overrightarrow{n}$ est orthogonal à deux vecteurs directeurs $\overrightarrow{CD}$ et $\overrightarrow{CE}$ du plan $(CDE)$
- En déduire une équation cartésienne du plan $(CDE)$.
Vecteur normal à un plan-équation cartésienne d'un plan
Dans l'espace muni d'un repère othonormé, $P$ est un plan de l'espace, un vecteur $\overrightarrow{n}$ normal à $P$ est un vecteur directeur d'une droite orthogonale à $P$.
Le vecteur $\overrightarrow{n}$ est un vecteur normal au plan $P$ passant par $A$ et $P$ est l'ensemble des points $M(x;y;z)$ vérifiant $\overrightarrow{AM}.\overrightarrow{n}=0$.
$ax+by+cz+d=0$ est une équation cartésienne de $P$ de vecteur normal $\overrightarrow{n}\begin{pmatrix} a\\ b\\ c \end{pmatrix}$$\overrightarrow{n}\begin{pmatrix} 1\\ 1\\ 1 \end{pmatrix}$ est un vecteur normal au plan $CDE)$ donc une équation de $(CDE)$ est de la forme $x+y+z+d=0$.
$C\in (CDE) \Longleftrightarrow x_C+y_C+x-z+d_C=0 \Longleftrightarrow 4+d=0 \Longleftrightarrow d=-4$.
- Le plan $P$ a pour équation $3y+z-6=0$
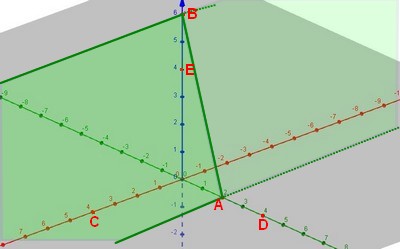
Montrer que la droite d'intersection de $P$ et du plan $(OIJ)$ est une droite $d$ passant par $A$ et parallèle à $(OI)$ et que le point $B$ appartient au plan $P$.
Représenter les traces (les droites d'intersection) de $P$ sur les plans de bases du repère.Si un point $M(x;y;z)$ appartient au plan $(OIJ)$ alors on a $z=0$Si Si un point $M(x;y;z)$ appartient au plan $(OIJ)$ alors $z=0$ et $M$ appartient au plan $P$ donc $3y+z-6=0$
donc $3y-6=0$ soit $y=2$
donc les points de la droite d'intersection de $P$ et de $(OIJ)$ ont pour coordonnées $(x;2;0)$ et donc cette droite est parallèle à $(OI)$ dans le plan $(O;I;J)$
$3y_B+z_B-6=3\times 0+6-6=0$ donc $B\in P$ .
- Justifier que les plans $P$ et $(CDE)$ sont sécants.
Il faut vérifier si les vecteurs normaux des plans $(CDE)$ et $P$ sont colinéaires$\overrightarrow{n}\begin{pmatrix} 1\\ 1\\ 1 \end{pmatrix}$ est un vecteur normal au plan $(CDE)$ et $\overrightarrow{n'}\begin{pmatrix} 0\\ 3\\ 1 \end{pmatrix}$ est un vecteur normal au plan $P$
$3y_{\overrightarrow{n}}=3\times 1=3=y_{\overrightarrow{n'}}$
mais $3x_{\overrightarrow{n}}=3\times 1=3\neq x_{\overrightarrow{n'}}$
donc les vecteurs normaux des plans $P$ et $(CDE)$ ne sont pas colinéaires
donc $P$ et $(CDE)$ ne sont pas parallèles
- Construire la droite $\Delta$ intersection de $P$ et $(CDE)$ sur le graphique.
Il faut chercher deux points d'intersectionnde $P$ et $(CDE)$Les droites $(AB)$ et $(ED)$ sont coplanaires et contenues dans le plan $(OJK)$ donc sécantes en $X$.
On peut de même trouver un point $Y$ du plan $(OIJ)$ appartenant à $P$ et $(CDE)$.
L'intersection $\Delta$ des deux plans sur le graphique est la droite $(XY)$.
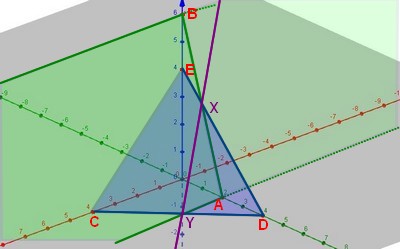
- Déterminer la représentation paramétrique de $\Delta$.
Les points d'intersection de $P$ et $(CDE)$ vérifient les équations des deux plans.
On peut exprimer $x$ et $z$ en fonction de $y$ par exempleLes points d'intersection de $P$ et $(CDE)$ vérifient les équations des deux plans donc on a $x+y+z-4=0$ et $3y+z-6=0$
$\begin{cases} x+y+z-4=0\\ 3y+z-6=0 \end{cases} \Longleftrightarrow \begin{cases} x=-y-z+4\\ z=-3y+6 \end{cases}$
$\phantom{\begin{cases} x+y+z-4=0\\ 3y+z-6=0 \end{cases}} \Longleftrightarrow \begin{cases} x=-y-(-3y+6)+4\\ z=-3y+6 \end{cases}$
$\phantom{\begin{cases} x+y+z-4=0\\ 3y+z-6=0 \end{cases}} \Longleftrightarrow \begin{cases} x=2y-2\\ z=-3y+6 \end{cases}$
donc en prenant $y=t$ on a $\begin{cases} x=2t-2\\ y=t\\ z=-3t+6 \end{cases}$
vidéos semblables
Pour compléter ce devoir, nous vous conseillons les vidéos suivantes pour préparer ce devoir.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.