1. Home
  2. chapitre 3 Dérivation-continuité-convexité
  3. exercice corrigé nº1185
PDF reservé aux abonnés
$f$ est une fonction définie et deux fois dérivable sur $\mathbb{R}$ définie par $f(x)=ax^3+6x^2-3x+1$ avec $a$ réel.
  1. Calculer la dérivée seconde $f~''$ de $f$

    Aide

    $a$ est le coefficient de $x^3$

    Solution

    $f~'(x)=a\times 3x^2+6\times 2x-3=3ax^2+12x-3$
    $f~''(x)=3a\times 2x+12=6x+12$
  2. En déduire la valeur de $a$ pour que fonction $f$ soit concave sur $[1;+\infty[$ et convexe $]-\infty;1]$

    Rappel de cours

    point d'inflexion et dérivée seconde

    si $f"(x)$ s'annule et change de signe en $x=x_A$ alors la courbe admet un point d'inflexion au point $A$.

    Aide

    Il faut résoudre l'équation $f~''(1)=0$

    Solution

    $f$ soit est concave sur $[1;+\infty[$ et convexe $]-\infty;1]$
    donc la dérivée seconde s'annule et change de signe en $x=1$
    $f~''(1)=0 \Longleftrightarrow 6a+12=0 \Longleftrightarrow a=-2$
  3. Déterminer l'équation de la tangente $T$ à la courbe au point d'abscisse $x=1$

    Rappel de cours

    Équation de la tangente au point d'abscisse $a$

    $f$ est une fonction définie et dérivable en $x=a$.
    La tangente à $C_f$ en $a$ a pour coefficient directeur $f'(a)$
    et pour équation réduite $ y=f'(a)(x-a)+f(a)$} cours

    Aide

    Calculer $f(1)$ puis $f'(1)$

    Solution

    $f(x)=-2x^3+6x^2-3x+1$
    $f(1)=-2+6-3+1=2$
    $f~'(x)=-2\times 3x^2+6\times 2x-3=-6x^2+12x-3$
    $f~'(1)=-6+12-3=3$
    $T$: $y=f~'(1)(x-1)+f(1)=3(x-1)+2=3x-1$
  4. Tracer la courbe représentative de $f$ et la tangente $T$ dans un repère orthogonal et contrôler les résultats obtenus

    Aide

    Avec GEOGEBRA, on peut saisir la fonction $f$ dans la barre de saisie puis tracer la tangente au point d'abscisse 1 en utilisant TANGENTE[1,$f$]
    Avec la calculatrice saisir $f$ dans Y1 et l'équation réduite de $T$ dans Y2

    Solution

    On peut utiliser GEOGEBRA pour contrôler le résultat.
    Avec GEOGEBRA, saisr la fonction $f$ dans la barre de saisie puis tracer la tangente au point d'abscisse 1 en utilisant TANGENTE[1,$f$]:


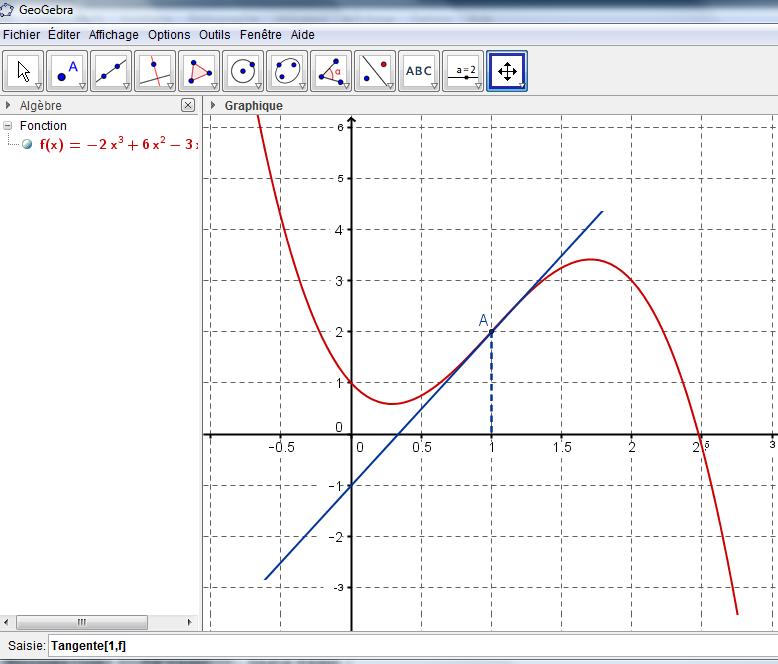
    Avec la calculatrice, saisir $f$ dans Y1 et l'équation réduite de $T$ dans Y2 et ne pas oublier de paramétrer le repère avec SHIFT F3 (V-WINDOW).
    \includegraphics[scale=0.6]{fig2}
    On peut zoomer sur le point d'inflexion pour contrôler cette portion du graphique:
    \includegraphics[scale=0.6]{fig3}
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
valider cet exercice
marquer cet exercice à revoir

Cours nº 1146


Vous pouvez retourner sur le cours après avoir vu cette vidéo.

Convexité et dérivée seconde

- dérivée seconde
- convexité et signe de la dérivée seconde
- point d'inflexion

infos cours

| 15-20mn
série 7 : Exercices de synthèse

retour sur le cours

vidéos semblables


Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
Convexité de f à partir de la courbe de la dérivée
| 6mnmn |

exercices semblables


Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.
Variations de la dérivée et convexité
| 5-7mn |