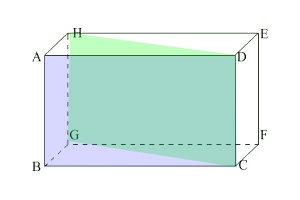
MATHS-LYCEE.FR exercice corrigé chapitre Géométrie dans l'espace

PDF reservé aux abonnés

$ABCDEFGH$ est un pavé droit.

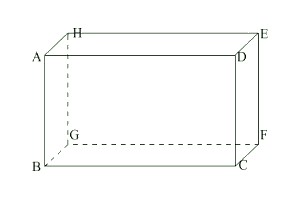
Donner la position relative des plans suivants:

$(ABC)$ et $(HGF)$

Rappel de cours

Position relative de deux plans
Les plans $P$ et $Q$ sont sécants
L'intersection est une droite

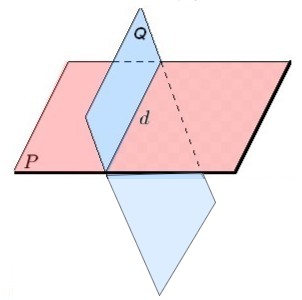
Les plans $P$ et $Q$ sont parallèles
Il existe deux droites sécantes de $P$ parallèles à deux droites sécantes de $Q$

Aide

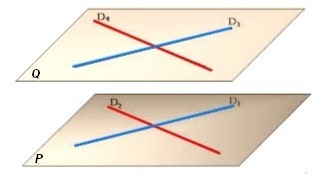On peut utiliser les droites parallèles du pavé droit

Solution

$ABGH$ est un rectangle donc $(AB)//(GH)$
et $BCFG$ est un rectangle donc $(BC)//(FG)$
On a donc deux droites sécantes $(AB)$ et $(BC)$ du plan $(ABC)$ parallèles à deux droites sécantes $(GH)$ et $(FG)$ du plan $(HGF)$
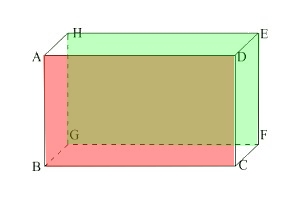
$(ABC)$ et $(DHG)$

Rappel de cours

Position relative de deux plans
Les plans $P$ et $Q$ sont sécants
L'intersection est une droite

Les plans $P$ et $Q$ sont parallèles
Il existe deux droites sécantes de $P$ parallèles à deux droites sécantes de $Q$

Aide

On peut utiliser les points $C$ et $D$.

Solution

La droite $(HG)$ est parallèle à la droite $(DC)$ donc les points $D$, $C$, $H$ et $G$ sont coplanaires
et le point $C$ appartient donc aux plans $(DHG)$ et $(ABC)$
de même le point $D$ appartient donc aux plans $(DHG)$ et $(ABC)$
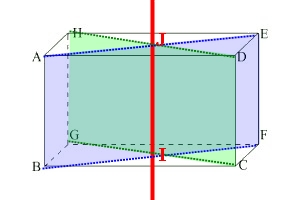
$(ABF)$ et $(HGC)$

Aide

On peut utiliser les droites $(HD)$ et $(AE)$.
et les droites $(BF)$ et $(GC)$.

Solution

Les droites $(AE)$ et $(BF)$ sont contenues dans le plan $(ABF)$
et les droites $(HD)$ et $(GC)$ sont contenues dans le plan $(HGC)$
$(AE)$ et $(HD)$ sont sécantes en $J$ (diagonales du rectangle $AHED$)
donc $J$ est un point d'intersection des plans $(ABF)$ et $(HGC)$

$(BF)$ et $(GC)$ sont sécantes en $I$ (diagonales du rectangle $BGFC$)
donc $I$ est un point d'intersection des plans $(ABF)$ et $(HGC)$