$ABCDEFGH$ est un cube(figure ci-dessous).
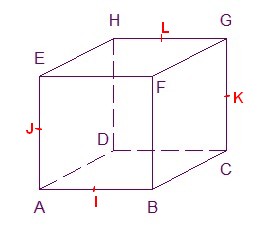
- Donner les coordonnées des sommets du cube dans le repère $(A;B;D;E)$?
Quelle est la nature de ce repère?$(AB)$ est l'axe des abscisses et $B(1;0;0)$...
Les côtés $[AB]$, $[AD]$ et $[AE]$ sont orthogonaux deux à deux et de même longueur.$A$ est l'origine du repère donc $A(0;0;0)$.
$(AB)$ défini l'axe des abscisses et $[AB]$ est l'unité de longueur donc $B(1;0;0)$.
De même, $D(0;1;0)$ et $E(0;0;1)$.
$C(1;1;0)$, $F(1;0;1)$, $G(1;1;1)$ (tracés en pointillés) et $H(0;1;1)$.
$ABCDEFGH$ est un cube donc les côtés $[AB]$, $[AD]$ et $[AE]$ sont orthogonaux deux à deux et de même longueur
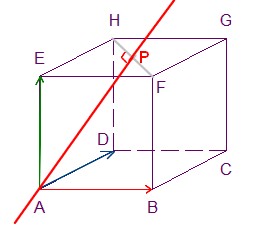
- Calculer les coordonnées de $P$ milieu de $[HF]$.
Coordonnées du milieu
L'espace est muni d'un repère quelconque.
Soit $A(x_A;y_A;z_A)$ et $B(x_B;y_B;z_B)$ Le milieu $I$ de $[AB]$ a pour coordonnées $\left(\dfrac{x_A+x_B}{2};\dfrac{y_A+y_B}{2};\dfrac{z_A+z_B}{2}\right)$$\begin{cases} x_P=\dfrac{x_H+x_F}{2}=\dfrac{1+0}{2}=\dfrac{1}{2}\\ y_P=\dfrac{y_H+y_F}{2}=\dfrac{0+1}{2}=\dfrac{1}{2}\\ z_P=\dfrac{z_H+z_F}{2}=\dfrac{1+1}{2}=1 \end{cases}$
- Les droites $(AP)$ et $(HF)$ sont-elles orthogonales?
Coordonnées d'un vecteur dans l'espace
L'espace est muni d'un repère quelconque.
Soit $A(x_A;y_A;z_A)$ et $B(x_B;y_B;z_B)$
$\overrightarrow{AB}\begin{pmatrix} x_B-x_A\\ y_B-y_A\\ z_B-z_A \end{pmatrix} $Produit scalaire dans un repère orthonormé de l'espace
Dans un repère orthonormé de l'espace, on a les vecteurs $\overrightarrow{u}\begin{pmatrix} x\\ y\\ z \end{pmatrix}$ et $\overrightarrow{v}\begin{pmatrix} x'\\ y'\\ z' \end{pmatrix}$.
$\overrightarrow{u}.\overrightarrow{v}=xx'+yy'+zz'$Orthogonalité et produit scalaire
Pour tous vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$, on a:
$\overrightarrow{u}.\overrightarrow{v}=0 \Longleftrightarrow \overrightarrow{u}=\overrightarrow{0}$ ou $\overrightarrow{v}=\overrightarrow{0}$ ou $\overrightarrow{u}$ et $\overrightarrow{v}$ sont orthogonaux.On peut calculer le produit scalaire $\overrightarrow{AP}.\overrightarrow{HF}$$\overrightarrow{AP}\begin{pmatrix} \dfrac{1}{2}\\ \dfrac{1}{2}\\ 1 \end{pmatrix}$ et $\overrightarrow{HF}\begin{pmatrix} 1\\ -1\\ 0 \end{pmatrix}$
$\overrightarrow{AP}.\overrightarrow{HF}=\dfrac{1}{2}\times 1+\dfrac{1}{2}\times (-1)=0$
donc les vecteurs directeurs $\overrightarrow{AP}$ de la droite $(AP)$ et $\overrightarrow{HF}$ de la droite $(HF)$ sont orthogonaux
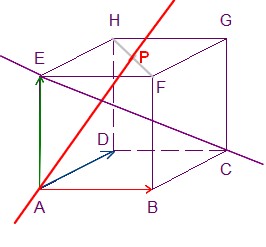
- Les droites $(AP)$ et $(EC)$ sont-elles orthogonales?
On peut calculer le produit scalaire $\overrightarrow{AP}.\overrightarrow{EC}$$\overrightarrow{AP}\begin{pmatrix} \dfrac{1}{2}\\ \dfrac{1}{2}\\ 1 \end{pmatrix}$ et $\overrightarrow{EC}\begin{pmatrix} 1\\ 1\\ -1 \end{pmatrix}$
$\overrightarrow{AP}.\overrightarrow{EC}=\dfrac{1}{2}\times 1+\dfrac{1}{2}\times (-1)+1\times (-1)1-1=0$
donc les vecteurs directeurs $\overrightarrow{AP}$ de la droite $(AP)$ et $\overrightarrow{EC}$ de la droite $(EC)$ sont orthogonaux
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 1393
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
Produit scalaire dans l'espace
- produit scalaire dans un repère
- orthogonalité et produit scalaire
infos cours
| 15mn
série 5 : Produit scalaire et coordonnées, orthogonalité dans l'espace
exercices semblables
Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.