Dans un repère orthonormé de l'espace, le plan $P$ a pour équation cartésienne $ax+by+cz+d=0$ et $A(x_A;y_A;z_A)$ est un point de l'espace.
On note $H$ l'intersection de la droite $\Delta$ passant par $A$ et orthogonale au plan $P$.
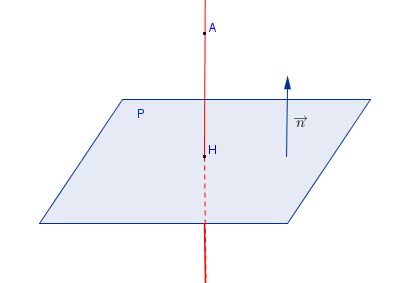
- Montrer que $\overrightarrow{n}.\overrightarrow{AH}=-ax_A-by_A-cz_A-d$ avec $\overrightarrow{n}\begin{pmatrix}
a\\
b\\
c
\end{pmatrix}$ vecteur normal au plan $P$
Vecteur normal à un plan-équation cartésienne d'un plan
Dans l'espace muni d'un repère othonormé, $P$ est un plan de l'espace, un vecteur $\overrightarrow{n}$ normal à $P$ est un vecteur directeur d'une droite orthogonale à $P$.
Le vecteur $\overrightarrow{n}$ est un vecteur normal au plan $P$ passant par $A$ et $P$ est l'ensemble des points $M(x;y;z)$ vérifiant $\overrightarrow{AM}.\overrightarrow{n}=0$.
$ax+by+cz+d=0$ est une équation cartésienne de $P$ de vecteur normal $\overrightarrow{n}\begin{pmatrix} a\\ b\\ c \end{pmatrix}$Produit scalaire dans un repère orthonormé de l'espace
Dans un repère orthonormé de l'espace, on a les vecteurs $\overrightarrow{u}\begin{pmatrix} x\\ y\\ z \end{pmatrix}$ et $\overrightarrow{v}\begin{pmatrix} x'\\ y'\\ z' \end{pmatrix}$.
$\overrightarrow{u}.\overrightarrow{v}=xx'+yy'+zz'$$H(x_H;y_H;z_H)$ appartient à $P$ donc $ax_H+by_H+cz_H+d=0$$\begin{cases} x_{\overrightarrow{AH}}=x_H-x_A\\ y_{\overrightarrow{AH}}=y_H-y_A\\ z_{\overrightarrow{AH}}=z_H-z_A \end{cases}$
$\overrightarrow{n}.\overrightarrow{AH}=a\times (x_H-x_A)+b(y_H-y_A)+c(z_H-z_A)$
$\phantom{\overrightarrow{n}.\overrightarrow{AH}}=ax_H-ax_A+by_H-by_A+cz_H-cz_A$
$\phantom{\overrightarrow{n}.\overrightarrow{AH}}=ax_H+by_H+cz_H-x_A-by_A-cz_A$
$H\in P$ donc $ax_H+by_H+cz_H+d=0$ soit $ax_H+by_H+cz_H=-d$
donc $\overrightarrow{n}.\overrightarrow{AH}=-d-ax_A-by_A-cz_A$
- Montrer que $|\overrightarrow{n}.\overrightarrow{AH}|=AH\sqrt{a^2+b^2+c^2}$.
Produit scalaire avec les projetés orthogonaux
Soit $A$, $B$ et $C$ trois points ($A$ et $B$ distincts) et $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$
Si $H$ est le projeté orthogonal de $C$ sur $(AB)$:
$\overrightarrow{u}.\overrightarrow{v}=AB\times AH$ si $\widehat{BAH}=0$ (soit $\widehat{BAC}$ aigu)
et $\overrightarrow{u}.\overrightarrow{v}=-AB\times AH$ si $\widehat{BAH}=\pi$ (soit $\widehat{BAC}$ obtus)Les vecteurs $\overrightarrow{AH}$ et $\overrightarrow{n}$ sont colinéaires donc $(\overrightarrow{n},\overrightarrow{AH})=0$ ($\pi$)
donc $cos(\overrightarrow{n},\overrightarrow{AH})=1$ ou bien $$cos(\overrightarrow{n},\overrightarrow{AH})-1$Si on pose $\overrightarrow{n}=\overrightarrow{AB}$, les vecteurs $\overrightarrow{n}$ donc $\overrightarrow{AB}$ et $\overrightarrow{AH}$ sont colinéaires et donc $A$, $B$ et $H$ sont alignés.
on a donc $cos(\widehat{BAC})=1$ ou $cos(\widehat{BAC})=-1$
donc $|cos(\widehat{BAC})|=1$
$\overrightarrow{n}.\overrightarrow{AH}=||\overrightarrow{n} ||\times AH cos (\widehat{BAC})$
$||\overrightarrow{n}||=\sqrt{a^2+b^2+c^2}$
donc $|\overrightarrow{n}.\overrightarrow{AH}|=||\overrightarrow{n} ||\times AH |cos (\widehat{BAC})|=AH\sqrt{a^2+b^2+c^2}$
- En déduire l'expression de $AH$ en fonction des coordonnées de $A$ et de $\overrightarrow{n}$.
Il faut utiliser les deux résultats précédents de $\overrightarrow{n}.\overrightarrow{AH}$$\overrightarrow{n}.\overrightarrow{AH}=-ax_A-by_A-cz_A-d$ soit $|\overrightarrow{n}.\overrightarrow{AH}|=|-ax_A-by_A-cz_A-d|=|ax_A+by_A+cz_A+d|$
et $|\overrightarrow{n}.\overrightarrow{AH}|=AH\sqrt{a^2+b^2+c^2}$
donc $ AH\sqrt{a^2+b^2+c^2}=|ax_A+by_A+cz_A+d|$
- Dans un repère orthonormé de l'espace, on donne $A(2;1;3)$, $B(3;4;1)$ et $C(4;-1;1)$.
- Montrer que le triangle $ABC$ est rectangle en $A$.
Coordonnées d'un vecteur dans l'espace
L'espace est muni d'un repère quelconque.
Soit $A(x_A;y_A;z_A)$ et $B(x_B;y_B;z_B)$
$\overrightarrow{AB}\begin{pmatrix} x_B-x_A\\ y_B-y_A\\ z_B-z_A \end{pmatrix} $Produit scalaire dans un repère orthonormé de l'espace
Dans un repère orthonormé de l'espace, on a les vecteurs $\overrightarrow{u}\begin{pmatrix} x\\ y\\ z \end{pmatrix}$ et $\overrightarrow{v}\begin{pmatrix} x'\\ y'\\ z' \end{pmatrix}$.
$\overrightarrow{u}.\overrightarrow{v}=xx'+yy'+zz'$Il faut vérifier que les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ sont colinéaires.$\begin{cases} x_{\overrightarrow{AB}}=x_B-x_A=3-2=1\\ y_{\overrightarrow{AB}}=y_B-y_A=4-1=3\\ z_{\overrightarrow{AB}}=z_B-z_A=1-3=-2 \end{cases}$
donc $\overrightarrow{AB}\begin{pmatrix} 1\\ 3\\ -2 \end{pmatrix} $
$\begin{cases} x_{\overrightarrow{AC}}=x_C-x_A=4-2=2\\ y_{\overrightarrow{AC}}=y_C-y_A=-1-1=-2\\ z_{\overrightarrow{AC}}=z_C-z_A=1-3=-2 \end{cases}$
donc $\overrightarrow{AC}\begin{pmatrix} 2\\ -2\\ -2 \end{pmatrix} $
$\overrightarrow{AB}.\overrightarrow{AC}=1\times 2+3\times (-2)+(-2)\times (-2)=2-6+4=0$
donc le vecteur $\overrightarrow{AB}$ est orthogonal au vecteur $\overrightarrow{AC}$
- Montrer que le vecteur $\overrightarrow{n}\begin{pmatrix}
5\\
1\\
4
\end{pmatrix}$ est un vecteur normal au plan $(ABC)$.
Il faut vérifier que le vecteur $\overrightarrow{n}$ est orthogonal aux vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$$\overrightarrow{AB}\begin{pmatrix} 1\\ 3\\ -2 \end{pmatrix} $ et $\overrightarrow{AC}\begin{pmatrix} 2\\ -2\\ -2 \end{pmatrix} $
donc $\overrightarrow{AB}.\overrightarrow{n}=1\times 5+3\times 1+(-2)\times 4=5+3-8=0$
et $\overrightarrow{AC}.\overrightarrow{n}=2\times 5+(-2)\times 1+(-2)\times 4=10-2-8=0$
donc le vecteur $\overrightarrow{n}$ est orthogonal aux vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ vecteurs directeurs du plan $(ABC)$
- Soit $D(4;4;6)$, calculer le volume du tétraèdre $ABCD$.
Distance dans l'espace
Si le repère de l'espace est orthonormé, la distance $AB$ est: $AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2+(z_B-z_A)^2}$Le volume d'un tétraèdre est donné par $V=\dfrac{\text{Aire de la bas}\times \text{hauteur}}{3}$
Il faut calculer la hauteur du tétraèdre c'est à dire la distance entre le point $D$ et le projeté orthognal $H$ de $D$ sur $(ABC)$On note $H$ le projeté orthogonal de $D$ sur le plan $(ABC)$
$ABCD$ est un triangle rectangle en $A$ donc l'aire de $ABC$ est $\mathcal{A}=\dfrac{AB\times AC}{2}$
$AB=\sqrt{x_{\overrightarrow{AB}}^2+y_{\overrightarrow{AB}}^2+z_{\overrightarrow{AB}}^2}=\sqrt{1^2+3^2+(-2)^2}=\sqrt{14}$
$AC=\sqrt{x_{\overrightarrow{AC}}^2+y_{\overrightarrow{AC}}^2+z_{\overrightarrow{AC}}^2}=\sqrt{2^2+(-2)^2+(-2)^2}=\sqrt{12}=2\sqrt{3}$
L'aire de $ABC$ est donc $\mathcal{A}=\dfrac{\sqrt{14}\times 2\sqrt{3}}{2}=\sqrt{14}\sqrt{3}=\sqrt{42}$
En utilisant la question 3, on a donc:
$DH=\dfrac{|ax_D+by_D+cz_D+d|}{\sqrt{a^2+b^2+c^2}} $
Il faut alors déterminer $d$ en cherchant une équation cartésienne du plan $(ABC)$.
On a $\overrightarrow{n}\begin{pmatrix} 5\\ 1\\ 4 \end{pmatrix}$ est un vecteur normal au plan $(ABC)$ donc $a=5$, $b=1$ et $c=4$
et une équation de $(ABC)$ est de la forme $5x+y+4z+d=0$
$A\in (ABC) \Longleftrightarrow 5x_A+y_A+4z_A+d=0$
$\phantom{A\in (ABC)} \Longleftrightarrow 5\times 2+1+4\times 3+d=0$
$\phantom{A\in (ABC)} \Longleftrightarrow 10+1+12+d=0$
$\phantom{A\in (ABC)} \Longleftrightarrow d=-23$
$DH=\dfrac{|5\times 4+1\times 4+4\times 6|}{\sqrt{5^2+1^2+4^2}}=\dfrac{48}{\sqrt{42}} $
$\mathcal{V}=\dfrac{\mathcal{A}\times DH}{3}$
$\phantom{\mathcal{V}}=\dfrac{\sqrt{42} \times \dfrac{48}{\sqrt{42}} }{3}$
$\phantom{\mathcal{V}}=\dfrac{48}{3}$
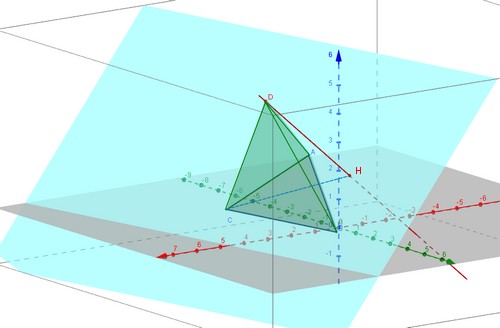
- Montrer que le triangle $ABC$ est rectangle en $A$.
Application
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 1403
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
Équation d'un plan
- points coplanaires dans un repère
- vecteur normal à un plan
- équation d'un plan
infos cours
| 15mn
série 9 : Exercices de synthèse
Fiche méthode
Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Equation cartésienne d'un plan
- vecteur normal
- déterminer une équation d'un plan
- position relative d'une droite et d'un plan
- intersection de droites et plans
infos: | 15-20mn |
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.