MATHS-LYCEELa fonction $f$ est définie sur $\mathbb{R}$ par $f(x)=2x^2-4x-6$ et on note $\mathcal{P}$ sa courbe représentative dans un repère orthogonal.
- Déterminer la forme canonique de $f$.
Forme canonique
Toute fonction polynôme de degré 2 définie sur $\mathbb{R}$ par $P (x) = ax^2 + bx + c$ peut s'écrire sous la forme $P (x) = a(x -\alpha)^2 + \beta$ avec $\alpha=\dfrac{-b}{2a}$ et $\beta= P ( \alpha)$.
Cette écriture de $P (x)$ est appelée forme canonique et $S(\alpha;\beta)$ est le sommet de la parabole représentant la fonction $P$Il faut alors calculer $\alpha$ et $\beta=f(\alpha)$ avec $a=2$, $b=-4$ et $c=-6$On a ici $a=2$, $b=-4$ et $c=-6$
donc $\alpha=\dfrac{-b}{2a}=\dfrac{-(-4)}{4}=1$
et $\beta=f(\alpha)=f(1)=2\times 1^2-4\times 1-6=-8$
- Dresser le tableau de variations de $f$
Variations fonction polynôme du second degré
Soit la fonction $P$ définie sur $\mathbb{R}$ par sa forme canonique $P (x) = a(x-\alpha)^2 + \beta$
La courbe représentative de $P$ est une parabole dont le sommet a pour coordonnées $(\alpha; \beta)$.
Tableau de variation: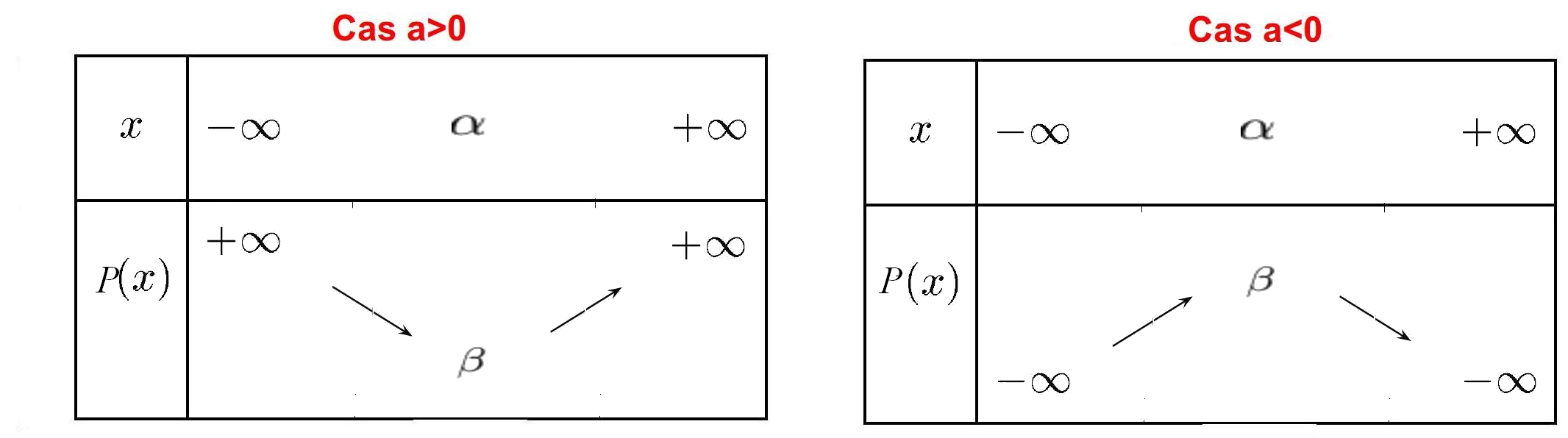
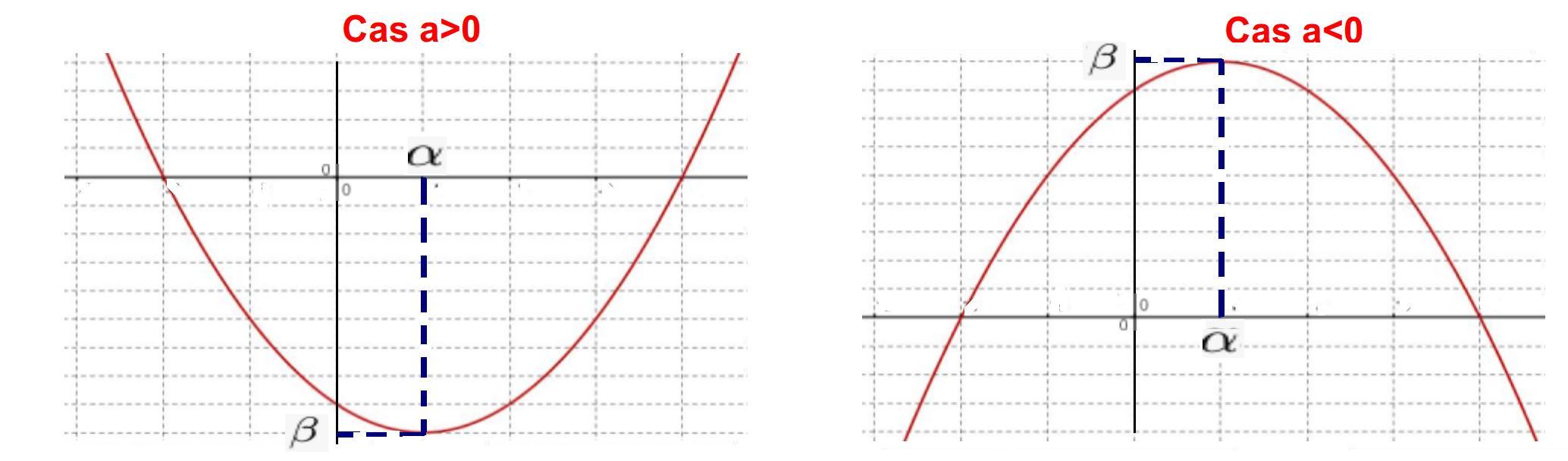Il faut alors calculer $\alpha$ et $\beta=f(\alpha)$ avec $a=2$, $b=-4$ et $c=-6$On a $\alpha=1$ et $\beta=-8$ donc le sommet de la parabole a pour coordonnées $(1;-8)$
et le coefficient $a$ de $x^2$ est $a=2$ donc positif, on a donc:
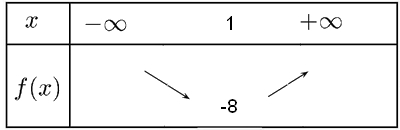
- Montrer que $x_1=-1$ et $x_2=3$ sont deux racines de $f$.
Racines
Les racines de $p(x)=ax^2+bx+c$ avec$a\neq 0$ sont les valeurs de $x$ annulant $P$
c'est à dire telles que $P(x)=0$.
$\Delta=b^2-4ac$
Si $\Delta>0$ donc il y a deux racine $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}$ et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}$
Si $\Delta=0$ il y a une racine (double) $x_1=\dfrac{-b}{2a}$
Si $\Delta<0$ il n'y a aucune racine
Remarque: Graphiquement, les racines sont les abscisses des points d'intersection de la parabole et de l'axe des abscisses.Il faut vérifier que $f(x_1)=0$$f(-1)=2\times (-1)^2-4\times (-1)-6$ ne pas oublier les parenthèses car$(-1)^2=1$ mais $-1^2=-1$
$~~~~=2+4-6$
$~~~~=0$
$f(3)=2\times 3^2-4\times 3-6$
$~~~~=18-12-6$
$~~~~=0$
- Vérifier que la forme factorisée de $f$ est $f(x)=a(x-x_1)(x-x_2)$.
Identités remarquables
$(a+b)^2=a^2+2ab+b^2$
$(a-b)^2=a^2-2ab+b^2$
$(a-b)(a+b)=a^2-b^2$
aide Remplacer $x_1$ et $x_2$ par les valeurs obtenues à la question précédente et vérifier que l'on obtient $2x^2-4x-6$ en développant.On a obtenu $x_1=-1$ et $x_2=3$.
$a(x-x_1)(x-x_2)=2(x-(-1))(x-3)$ $x-x_1=x-(-1)=x+1$
$\phantom{2(x+1)(x-3)}=2(x+1)(x-3)$
$\phantom{2(x+1)(x-3)}=2(x^2+x-3x-3)$
$\phantom{2(x+1)(x-3)}=2(x^2-2x-3)$
$\phantom{2(x+1)(x-3)}=2x^2-4x-6$
$\phantom{2(x+1)(x-3)}=f(x)$
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 591
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
Forme canonique, variations et équations
- forme canonique et sommet de la parabole
- variations de $P(x)=ax^2+bx+c$
- discriminant et racines
infos cours
| 10-15mn
série 0 : Racines et discriminant
exercices semblables
Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.