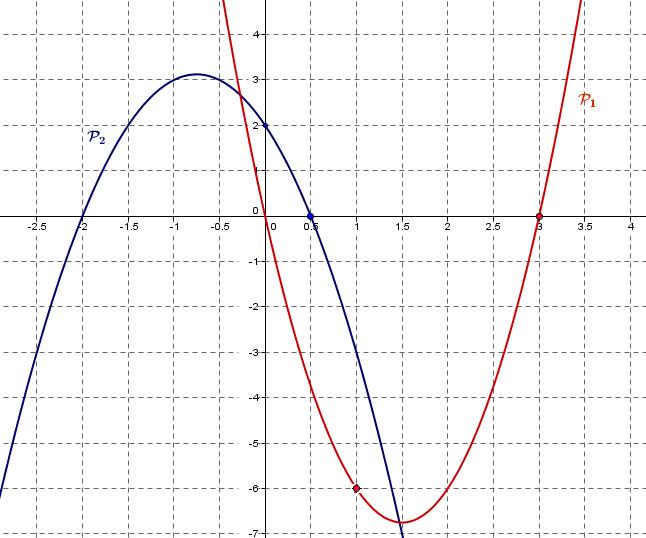
On donne ci-dessous les représentations graphiques $\mathcal{P}_1$ et $\mathcal{P}_2$ respectivement des fonctions polynômes de degré 2 $P$ et $Q$
Déterminer l'expression de chacune de ces fonctions sous forme factorisée puis sous forme développée et donner les coordonnées du sommet $S$ de la parabole.
- Pour $P$:
Forme factorisée
- Si le polynôme du second degré $P(x)=ax^2+bx+c$ (avec $a\neq 0$) admet deux racines $x_1$ et $x_2$
alors la forme factorisée de $P$ est $P(x)=a(x-x_1)(x-x_2)$
- Si le polynôme du second degré $P(x)=ax^2+bx+c$ (avec $a\neq 0$) admet une racine $x_1$
alors la forme factorisée de $P$ est $P(x)=a(x-x_1)^2$
- Si le polynôme du second degré $P(x)=ax^2+bx+c$ (avec $a\neq 0$) n'admet aucune racine
alors la forme factorisée de $P$ n'existe pasLire les coordonnées des points d'intersection de la parabole et de l'axe des abscisses (racines de $P$)
Utiliser les coordonnées d'un troisième point de la parabole pour déterminer le coefficient $a$La parabole $\mathcal{P}_1$ coupe l'axe des abscisses en $x_1=0$ et $x_2=3$
On peut donc écrire $f_1(x)=a(x-x_1)(x-x_2)=a(x-0)(x-3)=ax(x-3)$
La parabole $\mathcal{P}_1$ passe aussi par le point de coordonnées $(1;-6)$
On a donc $P(1)=a\times 1\times (1-3)=-2a=-6$
$ -2a=-6 \Longleftrightarrow a=3$
donc $P(x)=3x(x-3)$ (forme factorisée)
$P(x)=3x(x-3)=3x^2-9x$ (forme développée)
Coordonnées du sommet de la parabole $S(\alpha;\beta)$:
$\alpha=\dfrac{-b}{2a}=\dfrac{9}{6}=\dfrac{3}{2}$
$\beta=P(\alpha)=P\left(\dfrac{3}{2} \right)=3\times \left(\dfrac{3}{2}\right)^2-9\times \dfrac{3}{2}=\dfrac{27}{4}-\dfrac{27}{2}=\dfrac{27}{4}-\dfrac{54}{4}=\dfrac{-27}{4}$
donc $S\left(\dfrac{3}{2};\dfrac{-27}{4}\right)$
soit avec des coordonnées sous forme décimale $S(1,5~~;~~-6,75)$ pour contrôler le résultat sur le graphique.
- Pour $Q$:
La parabole $\mathcal{P}_2$ coupe l'axe des abscisses en $x_1=-2$ et $x_2=0,5$
On peut donc écrire $Q(x)=a(x-x_1)(x-x_2)=a(x-(-2))(x-0,5)=a(x+2)(x-0,5)$
La parabole $\mathcal{P}_2$ passe aussi par le point de coordonnées $(0;2)$
On a donc $Q(0)=a(0+2)(0-0,5)=-a=2$
donc $a=-2$
donc $Q(x)=-2(x+2)(x-0,5)$ (forme factorisée)
$Q(x)=-2(x+2)(x-0,5)=-2(x^2-0,5x+2x+2\times (-0,5))=-2(x^2+1,5x-1)=-2x^2-3x+2$ (forme développée)
Coordonnées du sommet de la parabole $S(\alpha;\beta)$:
$\alpha=\dfrac{-b}{2a}=\dfrac{3}{-4}=\dfrac{-3}{4}$
$\beta=Q(\alpha)$
$\phantom{\beta}=P\left(\dfrac{-3}{4} \right)$
$\phantom{\beta}=-2\times \left(\dfrac{-3}{4}\right)^2-3\times \dfrac{-3}{4}+2$
$\phantom{\beta}=\dfrac{-18}{16}+\dfrac{9}{4}+2$
$\phantom{\beta}=\dfrac{-9}{8}+\dfrac{18}{8}+\dfrac{16}{8}$
$\phantom{\beta}=\dfrac{25}{8}$
donc $S\left(\dfrac{-3}{4};\dfrac{25}{8}\right)$
soit avec des coordonnées sous forme décimale $S(-0,75~~;~~3,125)$ pour contrôler le résultat sur le graphique.
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 591
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
Forme canonique, variations et équations
- forme canonique et sommet de la parabole
- variations de $P(x)=ax^2+bx+c$
- discriminant et racines
infos cours
| 10-15mn
série 0 : Racines et discriminant
Fiche méthode
Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Rechercher l'expression de $f$
- connaissant le sommet
- connaissant les racines
- à partir de trois points
infos: | 8-12mn |
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.