MATHS-LYCEERésoudre les équations suivantes dans $]-\pi;\pi]$.
On pourra utiliser le cercle trigonométrique.
- $cos(x)=\dfrac{1}{2}$
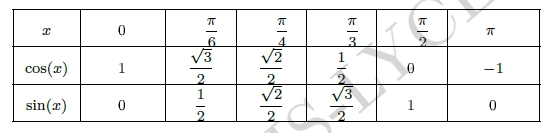
Valeurs remarquables du cos et du sin
Chercher une mesure $\alpha$ telle que $cos(\alpha)=\dfrac{1}{2}$
il y a deux valeurs de $x$ possibles donnant le même cosinus$cos(\dfrac{\pi}{3})=\dfrac{1}{2}$
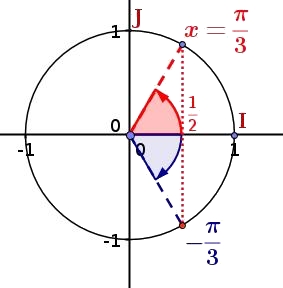
$cos(\dfrac{\pi}{3})=cos(\dfrac{-\pi}{3})=\dfrac{1}{2}$
Si la résolution se fait sur $\mathbb{R}$, il y a une infinité de solutions s'écrivant $\dfrac{\pi}{3}+k2\pi$ et $-\dfrac{\pi}{3}+k2\pi$ avec $k \in \mathbb{Z}$ ($k$ entier relatif) - $cos(x)=\dfrac{-\sqrt{3}}{2}$
Chercher une mesure $\alpha$ telle que $cos(\alpha)=\dfrac{\sqrt{3}}{2}$
En déduire les valeurs pour lesquelles $cos(x)=-\dfrac{\sqrt{3}}{2}$
Pour tout réel $x$, on a $cos(-x)=cos(x)$$cos(\dfrac{\pi}{6})=\dfrac{\sqrt{3}}{2}$
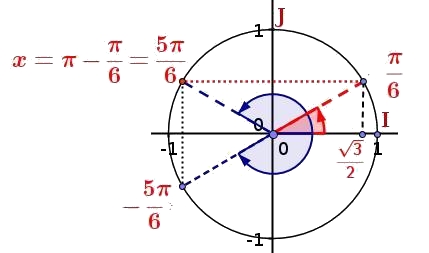
$cos(\dfrac{5\pi}{6})=cos(\dfrac{-5\pi}{6})=\dfrac{-\sqrt{3}}{2}$
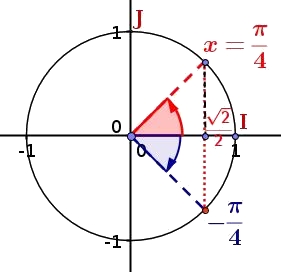
- $cos(x)=\dfrac{\sqrt{2}}{2}$
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 819
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
cosinus et sinus d'un angle (part 2)
- cosinus et sinus sur le cercle trigonométrique
- cos et sin des angles associés ($-x$, $\pi-x$...)
- valeurs remarquables du cos et sin
infos cours
| 15mn
série 4 : Équations trigonométriques
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.