Dans le plan muni d'un repère orthonormé, le point $A$ a pour coordonnées $(2;1)$ et on note $\mathcal{C}$ le cercle de centre $A$ et de rayon $r=\dfrac{5}{2}$. La droite $(d)$ a pour équation $2x-y+2=0$
- Déterminer une équation du cercle $\mathcal{C}$.
Équation d'un cercle
Dans un repère orthonormé, le cercle de centre $C(x_C;y_C)$ et de rayon $r$ a pour équation $(x-x_C)^2+(y-y_C)^2=r^2$Le cercle $\mathcal{C}$ admet pour équation $(x-x_A)^2+(y-y_A)^2=r^2$
- Tracer $\mathcal{C}$ puis $(d)$ dans un repère orthonormé et conjecturer le nombre de points d'intersection du cercle et de la droite et les coordonnées de ceux-ci.
On pourra faire la figure avec le logiciel GEOGEBRAaide GEOGEBRA
Placer A
Tracer le cercle avec la commande cercle défini par son centre et son rayon
Saisir l'équation de $(d)$ dans la barre de saisie (en bas de la fenêtre)
Marquer les points d'intersection avec la commande intersection de deux objets en pointant le cercle puis la droitefigure
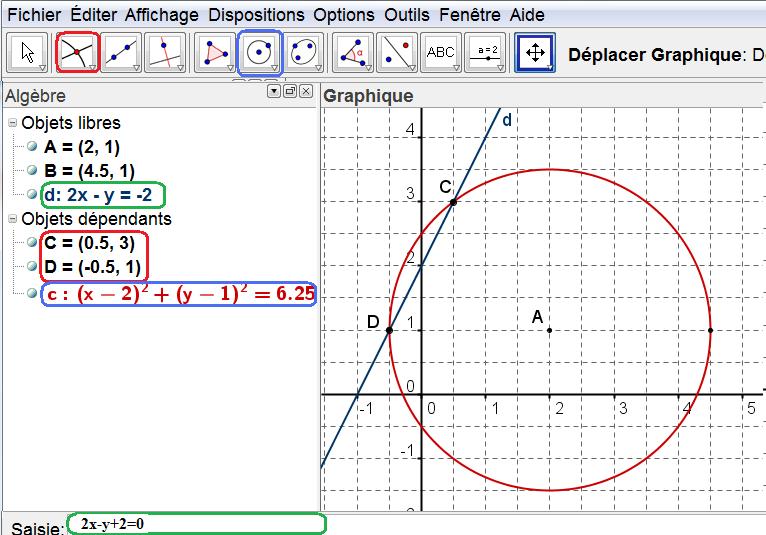
- Déterminer par le calcul les coordonnées des points d'intersection de $(d)$ et de $\mathcal{C}$.
Il faut résoudre un système de deux équations à deux inconnues formé avec lune équation du cercle et une équation de la droite
On peut isoler $y$ dans l'équation de la droite pour le remplacer dans l'équation du cercleLe point $M(x;y)$ appartient au cercle $\mathcal{C}$ et à la droite $(d)$ si ses coordonnées vérifient le système d'équations suivant:
$\phantom{\Longleftrightarrow }\begin{cases} (x-2)^2+(y-1)^2=\dfrac{25}{4} \\ 2x-y+2=0 \end{cases}$
$\Longleftrightarrow \begin{cases} (x-2)^2+(y-1)^2=\dfrac{25}{4} \\ 2x+2=y \end{cases}$
$\Longleftrightarrow \begin{cases} (x-2)^2+(2x+2-1)^2=\dfrac{25}{4} \\ 2x+2=y \end{cases}$
$\Longleftrightarrow \begin{cases} (x-2)^2+(2x+1)^2=\dfrac{25}{4} \\ 2x+2=y \end{cases}$
$\Longleftrightarrow \begin{cases} x^2-4x+4+4x^2+4x+1=\dfrac{25}{4} \\ 2x+2=y \end{cases}$
$\Longleftrightarrow \begin{cases} 5x^2+5=\dfrac{25}{4} \\ 2x+2=y \end{cases}$
$\Longleftrightarrow \begin{cases} 20x^2+20=25 ~~~~ \text{On multiplie les deux membres par 4} \\ 2x+2=y \end{cases}$
$\Longleftrightarrow \begin{cases} x^2=\dfrac{1}{4} \\ 2x+2=y \end{cases}$
$\Longleftrightarrow \begin{cases} x=\dfrac{1}{2} \\ y =2\times \dfrac{1}{2}+2 \end{cases}$ ou bien $\begin{cases} x=\dfrac{-1}{2} \\ y =2\times \dfrac{-1}{2}+2 \end{cases}$
$\Longleftrightarrow \begin{cases} x=\dfrac{1}{2} \\ y =3 \end{cases}$ ou bien $\begin{cases} x=\dfrac{-1}{2} \\ y =1 \end{cases}$
Ceci est cohérent avec la conjecture observée sur la figure faite avec GEOGEBRA
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 906
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
Équation d'un cercle dans un repère orthonormé
- équation d'un cercle connaissant un diamètre
- équation d'un cercle connaissant le centre et le rayon
- déterminer le centre et le rayon d'un cercle
infos cours
| 10mn
série 4 : Cercles
Fiche méthode
Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Équation d'un cercle
- déterminer une équation de cercle
- déterminer le centre et le rayon connaissant une équation du cercle
infos: | mn |
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.