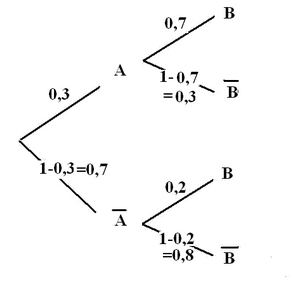
$A$ et $B$ sont deux événements.
La probabilité que l'événement $A$ soit réalisé est $0,3$.
La probabilité que l'événement $B$ soit réalisé sachant que $A$ est réalisé est $0,7$.
La probabilité que l'événement $B$ soit réalisé sachant que $A$ n'est pas réalisé est $0,2$.
- Construire un arbre pondéré correspondant aux différents cas possibles.
Événements indépendants
Deux événements $A$ et $B$ sont indépendants si $p(A\cap B)=p(A)\times p(B)$
Soient $A$ et $B$ deux événements tels que $p(A)\neq 0$ et $p(B)\neq 0$.
$A$ et $B$ sont indépendants $\Longleftrightarrow p_A(B)=p(B) \Longleftrightarrow p_B(A)=p(A)$Traduire les données de l'énoncé avec les notations des probabilités.La probabilité que l'événement $A$ soit réalisé est $0,3$ donc $p(A)=0,3$.
La probabilité que l'événement $B$ soit réalisé sachant que $A$ est réalisé est $0,7$ donc $p_A(B)=0,7$.
La probabilité que l'événement $B$ soit réalisé sachant que $A$ n'est pas réalisé est $0,2$ donc $p_{\overline{A}}(B)=0,2$ donc $p_{\overline{A}}(B)=0,2$.
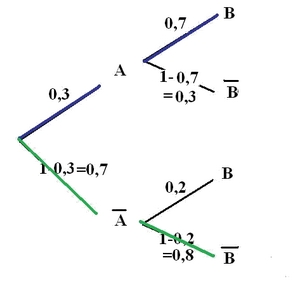
- A partir de l'arbre et en écrivant les formules utilisées, calculer $p(A\cap B)$ puis $p(\overline{A}\cap B)$.
Probabilité de l'événement $A\cap B$
Soient $A$ et $B$ deux événements avec $p(A)\neq 0$, on a
$p(A\cap B)=p(A)\times p_A(B)$Identifier le parcours sur l'arbre correspondant aux événements $A\cap B$ et $\overline{A} \cap B$ puis effectuer le produit des coefficients$p(A\cap B)=p(A)\times p_A(B)=0,3\times 0,7=0,21$ (parcours bleu sur l'arbre)
$p(\overline{A} \cap B)=p(\overline{A} )\times p_{\overline{A}}(B)=0,7\times 0,2=0,14$ (parcours vert sur l'arbre)
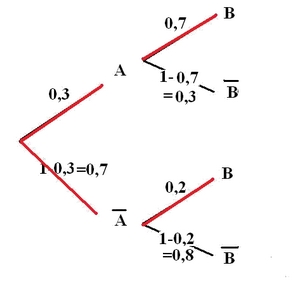
- Calculer $p(B)$.
Probabilités totales
Soient $A_1$, $A_2$,...$A_n$ des événements de l'univers $\Omega$ tels que $p(A_1)\neq 0$, $p(A_2)\neq 0$...$p(A_n)\neq 0$ et $B$ un événements.
Si $A_1$, $A_2$,...$A_n$ sont deux à deux disjoints et que leur réunion forme l'univers $\Omega$ alors $A_1$, $A_2$...$A_n$ forment une partition de $\Omega$
et on a $p(B)=p(A_1\cap B)+p(A_2\cap B)+...+p(A_n\cap B)$}
$A$ et $\overline{A}$ forment une partition de l'univers et on a $p(B)=p(A\cap B)+p(\overline{A}\cap B)$Identifier sur l'abre tous les parcours menant à l'événement B$A$ et $\overline{A}$sont disjoints et $A\cup \overline{A}=\Omega$
donc $A$ et $\overline{A}$ forment une partition de l'univers
En utilisant la formule des probabilités totales, on a:
$p(B)=p(A\cap B)+p(\overline{A}\cap B)=0,21+0,14=0,35$ (parcours rouges sur l'arbre)
- En déduire $p_B(A)$.
Probabilité conditionnelle
Soient $A$ et $B$ deux événements avec $p(A)\neq 0$.
La probabilité que l'événement $B$ soit réalisé sachant que l'événement $B$ est réalisé se note $p_A(B)$
et on a $p_A(B)=\dfrac{p(A\cap B)}{p(A)}$.On ne peut déterminer cette probabilité sans la formule des probabilités conditionnelles car on a dans l'arbre $p_A(B)$ et non $p_B(A)$$p_B(A)=\dfrac{p(A\cap B)}{p(B)}=\dfrac{0,21}{0,35}=\dfrac{21}{35}=\dfrac{3}{5}=0,6$
On ne peut déterminer cette probabilité sans la formule des probabilités conditionnelles car on a dans l'arbre $p_A(B)$ et non $p_B(A)$
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 945
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
Probabilités conditionnelles et probabilités totales
- calcul d'une probabilité conditionnelle
- partition et formule des probabilités totales
- événements indépendants
infos cours
| 10-15mn
série 2 : Arbres pondérés et probabilités totales
Fiche méthode
Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.
calculs de probabilités
- calcul de probabilités avec un arbre
- probabilités conditionnelles
- probabilités totales
infos: | 10-15mn |
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.