Pour chaque cas ci-dessous, étudier les variations de la suite $(u_n)$ définie pour tout $n\in \mathbb{N}$ en utilisant la fonction associée à la suite $(u_n)$.
- $u_{n}=2n^2+3n-5$
Variations fonction polynôme du second degré
Soit la fonction $P$ définie sur $\mathbb{R}$ par sa forme canonique $P (x) = a(x-\alpha)^2 + \beta$
La courbe représentative de $P$ est une parabole dont le sommet a pour coordonnées $(\alpha; \beta)$.
Tableau de variation: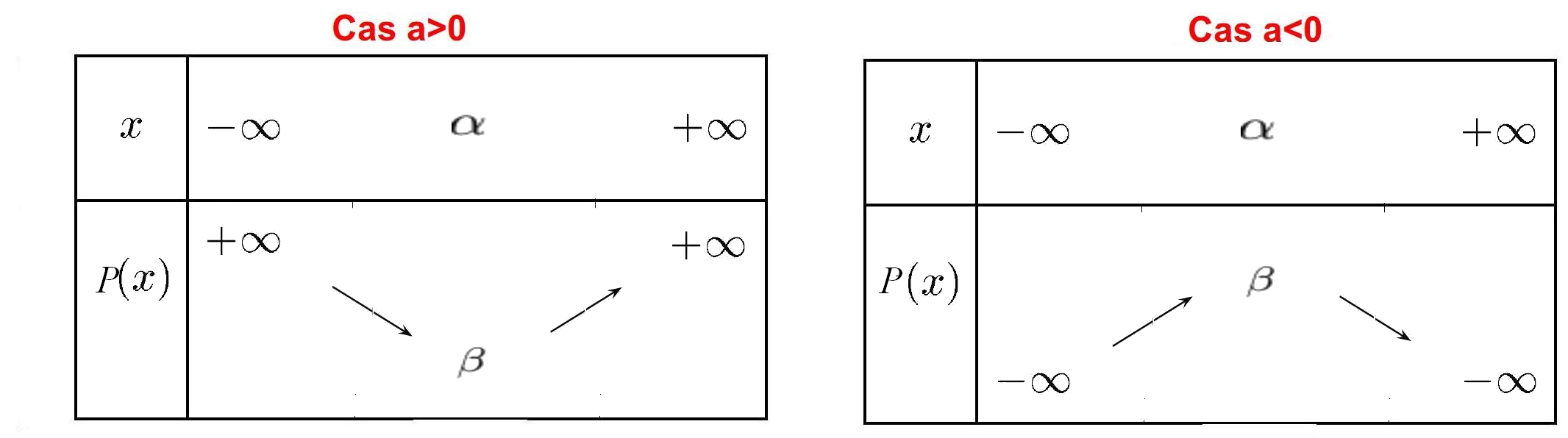
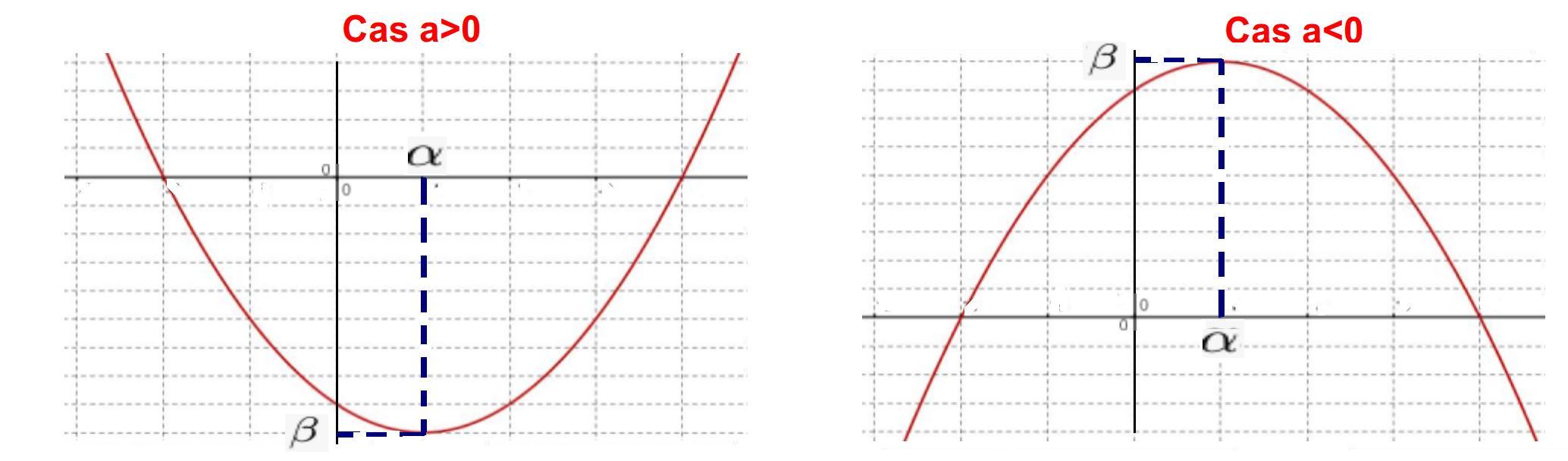 On peut chercher l'abscisse du sommet puis les variations de la fonction associée à $(u_n)$On pose $f$ définie sur $[0;+\infty[$ par $f(x)=2x^2+3x-5$.
On peut chercher l'abscisse du sommet puis les variations de la fonction associée à $(u_n)$On pose $f$ définie sur $[0;+\infty[$ par $f(x)=2x^2+3x-5$.
On a alors $u_n=f(n)=2n^2-3n-5$ et $f$ est la fonction associée à la suite $(u_n)$. Le sommet de la parabole a pour abscisse $\alpha=\dfrac{-b}{2a}=\dfrac{-3}{4}$
Le coefficient $a=2$ de $x^2$ est positif (parabole à l'endroit)
donc $f$ est croissante pour $x\geq \dfrac{-3}{4}$ donc sur $[0;+\infty[$
Si le chapitre dérivation a été traité:
$f$ est dérivable sur $[0;+\infty[$ (fonction polynôme du second degré).
$f'(x)=2\times 2x+3=4x+3$
$x \geq 0$ donc $4x+3 >0$ et $f'(x) >0$
donc $f$ est strictement croissante sur $[0;+\infty[$
- $u_{n}=\dfrac{-2}{n+1}$
Il faut étudier le signe de la dérivée de $f$ définie sur $[0;+\infty[$ telle que $u_n=f(n)$.
$f(x)=-2\times \dfrac{1}{x+1}$ (formule de dérivation $\dfrac{1}{v}$)On pose $f$ définie sur $[0;+\infty[$ par $f(x)=\frac{-2}{x+1}$.
On a alors $u_n=f(n)=\dfrac{-2}{n+1}$ et $f$ est la fonction associée à la suite $(u_n)$.
$f$ est dérivable sur $[0;+\infty[$ (quotient de fonctions dérivables).
$f(x)=-2\times \dfrac{1}{x+1}$
On pose $v(x)=x+1$ et on a $v'(x)=1$
$f'(x)=-2\times \dfrac{-v'(x)}{(v(x))^2}$
$\phantom{f'(x)}=-2\times \dfrac{-1}{(x+1)^2}$
$\phantom{f'(x)}= \dfrac{2}{(x+1)^2}$
$(x+1)^2 >0$ donc $f'(x) >0$
donc $f$ est strictement croissante sur $[0;+\infty[$
- $u_{n}=\dfrac{1-n}{n+2}$
Il faut étudier le signe de la dérivée de $f$ définie sur $[0;+\infty[$ telle que $u_n=f(n)$.
Pour dériver $f$, on pose $u(x)=1-x$ et $v(x)=x+2$On pose $f$ définie sur $[0;+\infty[$ par $f(x)=\dfrac{1-x}{x+2}$.
On a alors $u_n=f(n)=\dfrac{1-n}{n+2}$ et $f$ est la fonction associée à la suite $(u_n)$.
$f$ est dérivable sur $[0;+\infty[$ (quotient de fonctions dérivables).
On pose $u(x)=1-x$ et $v(x)=x+2$
et on a $u'(x)=-1$ et $v'(x)=1$
$f'(x)=\dfrac{u'(x)v(x)-u(x)v'(x)}{(v(x))^2}$
$\phantom{f'(x)}=\dfrac{-1\times (x+2)-(1-x)}{(x+2 )^2}$
$\phantom{f'(x)}=\dfrac{-x-2-1+x}{(x+2 )^2}$
$\phantom{f'(x)}=\dfrac{-3}{(x+2 )^2}$
$(x+2)^2 >0$ donc $f'(x) < 0$
donc $f$ est strictement décroissante sur $[0;+\infty[$
devoir nº 1087
Vous pouvez retourner sur le devoir après avoir vu cet exercice
Devoir sur les limites typoe BAC
- fonction associée à une suite
- variations d'une suite
- limite d'une suite majorée
- algorithme
infos cours
| mn