1. Home
  2. chapitre 2 Limites de fonctions
  3. exercice corrigé nº1130
PDF reservé aux abonnés
Déterminer les limites suivantes et interpréter graphiquement quand cela est possible.
  1. $\displaystyle \lim_{x \rightarrow +\infty} e^x+x$ et $\displaystyle \lim_{x \rightarrow -\infty} e^x+x$

    Rappel de cours

    limites usuelles

    $\displaystyle \lim_{x \rightarrow +\infty}x^n=+\infty$ ($n\in \mathbb{N}^*$)
    $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{1}{x^n}=0$ ($n\in \mathbb{N}^*$)
    $\displaystyle \lim_{x \rightarrow 0}\dfrac{1}{x^n}=\pm \infty$ ($n\in \mathbb{N}^*$)
    Limites de la fonction exponentielle(vue en première)
    $\displaystyle \lim_{x \rightarrow -\infty}e^x=0$
    $\displaystyle \lim_{x \rightarrow +\infty}e^x=+\infty$ $\displaystyle \lim_{x \rightarrow -\infty}x^n=\pm \infty$ ($n\in \mathbb{N}^*$)
    $\displaystyle \lim_{x \rightarrow -\infty}\dfrac{1}{x^n}=0$ ($n\in \mathbb{N}^*$)
    $\displaystyle \lim_{x \rightarrow +\infty}\sqrt{x}=+ \infty$ ($n\in \mathbb{N}^*$)
    Limites de la fonction $ln$ (chapitre fonction $ln$)
    $\displaystyle \lim_{x \rightarrow 0^+}ln(x)=-\infty$
    $\displaystyle \lim_{x \rightarrow +\infty}ln(x)=+\infty$

    Aide

    Il n'y a pas indétermination donc on cherche la limite de chaque terme.

    Solution

    $\displaystyle \lim_{x \rightarrow +\infty} e^x=+\infty$ et $\displaystyle \lim_{x \rightarrow +\infty} x=+\infty$

    $\displaystyle \lim_{x \rightarrow -\infty} e^x=0$ et $\displaystyle \lim_{x \rightarrow -\infty} x=-\infty$
  2. $\displaystyle \lim_{x \rightarrow +\infty} \dfrac{1}{e^x+1}$ et $\displaystyle \lim_{x \rightarrow -\infty} \dfrac{1}{e^x+1}$

    Rappel de cours

    Opérations sur les limites

    Aide

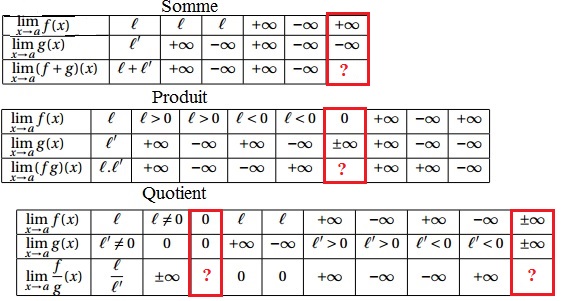    Il n'y a pas indétermination donc on cherche la limite du dénominateur puis du quotient

    Solution

    $\displaystyle \lim_{x \rightarrow +\infty} e^x=+\infty$ donc $\displaystyle \lim_{x \rightarrow +\infty} e^x+1=+\infty$

    La représentation graphique de $f$ admet donc une asymptote d'équation $y=0$ (axe des abscisses) en $+\infty$.
    $\displaystyle \lim_{x \rightarrow -\infty} e^x=0$ et $\displaystyle \lim_{x \rightarrow -\infty} e^x+1=1$

    La représentation graphique de $f$ admet donc une asymptote d'équation $y=1$ (axe des abscisses) en $-\infty$.
  3. $\displaystyle \lim_{x \rightarrow +\infty} x^2e^x$ et $\displaystyle \lim_{x \rightarrow -\infty} \dfrac{e^x}{x}$

    Rappel de cours

    Opérations sur les limites

    Solution

    $\displaystyle \lim_{x \rightarrow +\infty} e^x=+\infty$ donc $\displaystyle \lim_{x \rightarrow +\infty} x^2=+\infty$

    $\displaystyle \lim_{x \rightarrow -\infty} e^x=0$ et $\displaystyle \lim_{x \rightarrow -\infty} x=-\infty$

    La représentation graphique de $f$ admet donc une asymptote d'équation $y=0$ (axe des abscisses) en $-\infty$.

devoir nº 1134


Vous pouvez retourner sur le devoir après avoir vu cet exercice

Premier bilan sur les limites

- opérations sur les limites
- limites avec les fonctions usuelles
- limites avec exponentielle et croissances comparées

infos cours

| 30mn

retour sur le devoir