La fonction $f$ définie et deux fois dérivable sur $]0;+\infty[$ par $f(x)=ax+bln(x)$ avec $a$ et $b$ réels.
On donne ci-dessous $C_f$ la représentation graphique de $f$ dans un repère orthogonal et T la tangente à la courbe au point $A$ d'abscisse 1.
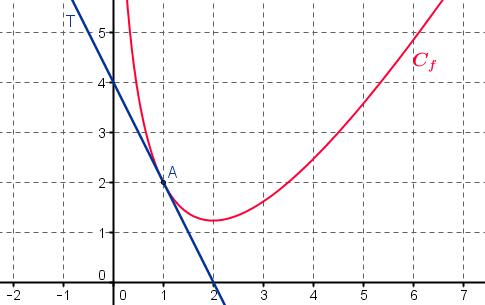
- Déterminer graphiquement $f(1)$ et $f~'(1)$
Équation de la tangente au point d'abscisse $a$
$f$ est une fonction définie et dérivable en $x=a$.
La tangente à $C_f$ en $a$ a pour coefficient directeur $f'(a)$
et pour équation réduite $ y=f'(a)(x-a)+f(a)$}Il faut déterminer le coefficient directeur de T.Le point $A$ a pour coordonnées $(1;2)$ et appartient à la courbe
donc $f(1)=2$
$f~'(1)$ est le coefficient directeur de la tangente T à la courbe au point $A$ d'abscisse 1 T passe par $A(1;2)$ et par $B(0;4)$
donc $f~'(1)=\dfrac{y_B-y_A}{x_B-x_A}=\dfrac{4-2}{0-1}=-2$
- Exprimer $f~'(x)$ en fonction de $a$ et $b$.
Dérivée de la fonction ln
La fonction $ln$ est dérivable sur $]0;+\infty[$ et $(ln(x))'=\dfrac{1}{x}$On a $f(x)=ax+b\times ln(x)$
donc $f~'(x)=a+b\times \dfrac{1}{x}=a+\dfrac{b}{x}$
- En utilisant la question 1, déterminer les réels $a$ et $b$.
On a $f(1)=2$ et il faut exprimer $f(x)$ en fonction de $a$ et $b$.
De même on a $f~'(1)=-2$ et il faut exprimer $f~'(1)$ en fonction de $a$ et $b$.
Rappel: $ln(1)=0$$f(x)=ax+bln(x)$ donc $f(1)=a+bln(1)=a$
et d'après la question 1, $f(1)=2$
donc $a=2$
$f~'(x)=a+\dfrac{b}{x}$ donc $f~'(1)=a+b$
et d'après la question 1, $f~'(1)=-2$
donc $a+b=-2$
En remplaçant $a$ par 2, on a $2+b=-2$ donc $b=-4$
- Déterminer alors les variations de $f$.
On a obtenu à la question 2., $f~'(x)=a+\dfrac{b}{x}$ avec $a=2$ et $b=-4$
Il faut étudier le signe de $f~'(x)$ en réduisant au préalable au même dénominateur
Rappel: $x\in ]0;+\infty[$ donc $x>0$ ....D'après les questions 2. et 3., $f~'(x)=a+\dfrac{b}{x}$ avec $a=2$ et $b=-4$
donc $f~'(x)=2-\dfrac{4}{x}=\dfrac{2x-4}{x}$
$x\in ]0;+\infty[$ donc $x>0$ et $f~'(x)$ est du signe de son numérateur $2x-4$.
$2x-4>0 \Longleftrightarrow 2x>4 \Longleftrightarrow x>2$
donc $f~'(x)>0$ pour $x\in ]2;+\infty[$
- Calculer $f~''(x)$ et en déduire la convexité de $f$.
Signe de la dérivée seconde
Soit $f$ définie et dérivable sur un intervalle I de $\mathbb{R}$
si $f''(x)>0$ sur $I$ alors $f$ est convexe
si $f''(x)<0$ sur $I$ alors $f$ est concaveOn a $f~'(x)=\dfrac{2x-4}{x}$
On pose $u(x)=2x-4$ et $v(x)=x$$f~'(x)=\dfrac{2x-4}{x}$
On pose $u(x)=2x-4$ et $v(x)=x$
et on a $u'(x)=2$ et $v'(x)=1$
$f~'(x)=\dfrac{u'(x)v(x)-u(x)v'(x)}{(v(x))^2}$
$\phantom{f~'(x)}=\dfrac{2x-(2x-4)\times 1}{x^2}$ au signe $-$ devant la parenthèse
$\phantom{f~'(x)}=\dfrac{2x-2x+4}{x^2}$
$\phantom{f~'(x)}=\dfrac{4}{x^2}$
$x^2>0$ donc $f~''(x)$ est du signe de son numérateur
donc $f~''(x)>0$
Le résultat semble cohérent avec le tracé de $C_f$ donné, la courbe est au-dessus de ses tangentes.
devoir nº 1241
Vous pouvez retourner sur le devoir après avoir vu cet exercice
Étude de fonction et convexité
- nombre dérivé et lecture graphique
- limites avec ln et croissances comparées en +oo
- dérivée et variations
- dérivée seconde et convexité
infos cours
| 30mn