1. Home
  2. chapitre 6 Primitives et intégrales
  3. exercice corrigé nº1261
PDF reservé aux abonnés
Déterminer une primitive $F$ de $f$ sur $D$.
  1. $f(x)=x^3+1$ avec $D=\mathbb{R}$

    Rappel de cours

    Primitives des fonctions usuelles

    Solution

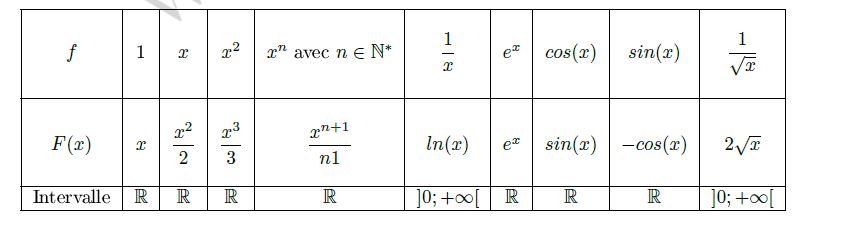    $f$ est continue sur $\mathbb{R}$ donc $f$ admet des primitives $f$.
    $F(x)=\dfrac{x^4}{4}+x$
    En effet $F'(x)=\dfrac{4x^3}{4}+1=x^3+1=f(x)$
  2. $f(x)=\dfrac{2}{x}$ avec $D=]0;+\infty[$

    Rappel de cours

    Primitives des fonctions usuelles

    Solution

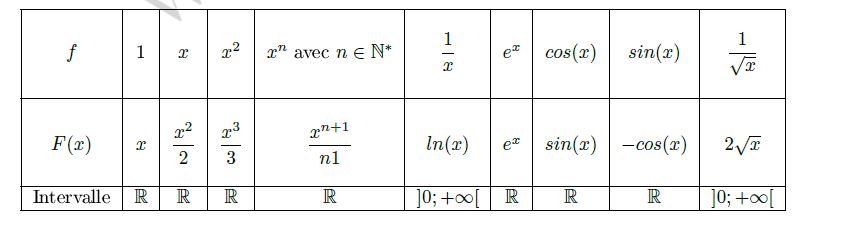    $f$ est continue sur $D$ donc admet des primitives sur $D$.
    $F(x)=2ln(x)$
    En effet $F'(x)=2\times \dfrac{1}{x}=\dfrac{2}{x}=f(x)$
  3. $f(x)=3e^x+1$ avec $D=\mathbb{R}$

    Aide

    On peut chercher une primitive de $3e^x$ et de $1$

    Solution

    $f$ est continue sur $D$ donc admet des primitives sur $D$.
    $F(x)=3e^x+x$
    En effet $F'(x)=3\times e^x+1=f(x)$

devoir nº 1289


Vous pouvez retourner sur le devoir après avoir vu cet exercice

Interrogation sur les primitives

- primitives des fonctions usuelles
- primitives de $e^{ax}$ et de $sin(ax+b)$
- justifier que F est une primitive de f
- déterminer la primitive vérifiant une condition donnée

infos cours

| mn

retour sur le devoir