1. Home
  2. chapitre 10 Maths expertes complexes
  3. exercice corrigé nº1456
PDF reservé aux abonnés
Le plan est muni d'un repère orthonormé.
  1. Déterminer l'ensemble $\mathcal{E}$ des points $M$ d'affixe $z$ tels que $|z-2+i|=3$.

    Rappel de cours

    Distances et modules

    Soient $A$ et $B$ d'affixes respectives $z_A$ et $z_B$.
    $AB=|z_B-z_A|$

    Aide

    On peut poser $z_A=2-i$ et on a alors $|z-z_A|=3$

    Solution

    $|z-2+i|=|z-(2-i)|$.
    On note $A$ le point d'affixe $z_A=2-i$ et on a alors $AM=|z-z_A|=|z-2+i|=3$
    1. Déterminer l'ensemble $\mathcal{E}_1$ des points $M$ tels que $|z-3+i|=|z+2-3i|$ par le calcul en posant $z=x+iy$ avec $x$ et $y$ réels.

      Rappel de cours

      Module d'un complexe

      Soit $M$ d'affixe $z$.
      Le module de $z=x+iy$ ($x$ et $y$ réels) noté $|z|$ est $|z|=OM=\sqrt{x^2+y^2}$.

      Aide

      $|z-3+i|=|x+iy-3+i|=|(x-3)+i(y+1)|$

      Solution

      $|z-3+i|=|x+iy-3+i|=|(x-3)+i(y+1)|=\sqrt{(x-3)^2+(y+1)^2}$
      $|z+2-3i|=|x+iy+2-3i|=|(x+2)+i(y-3)|=\sqrt{(x+2)^2+(y-3)^2}$
      $|z-3+i|=|z+2-3i|\Longleftrightarrow |z-3+i|^2=|z+2-3i|^2$
      $\phantom{|z-3+i|=|z+2-3i|}\Longleftrightarrow (x-3)^2+(y+1)^2=(x+2)^2+(y-3)^2$
      $\phantom{|z-3+i|=|z+2-3i|}\Longleftrightarrow x^2-6x+9+y^2+2y+1=x^2+4x+4+y^2-6y+9$
      $\phantom{|z-3+i|=|z+2-3i|}\Longleftrightarrow -6x+2y+1=4x+4-6y$
      $\phantom{|z-3+i|=|z+2-3i|}\Longleftrightarrow -10x+8y-3=0$
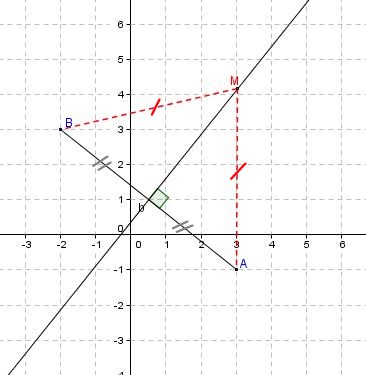
    2. Retrouver ce résultat géométriquement en utilisant les points $A$ et $B$ d'affixes respectives $z_A=3-i$ et $z_B=-2+3i$.

      Aide

      $AM=|z-z_A|=|z-(3-i)|=|z-3+i|$

      Solution

      $A$ a pour affixe $z_A=3-i$
      donc $AM=|z-z_A|=|z-(3-i)|=|z-3+i|$
      $B$ a pour affixe $z_B=-2+3i$
      donc $BM=|z-z_B|=|z-(-2+3i)|=|z+2-3i|$
      On veut donc $AM=BM$ et l'ensemble des points équidistants de $A$ et de $B$ est la médiatrice de $[AB]$.

devoir nº 1475


Vous pouvez retourner sur le devoir après avoir vu cet exercice

Devoir complet fin de chapitre

- conjugué et forme algébrique d'un quotient
- équations avec des complexes - recherche d'un ensemble de points (modules égaux)
- suites et complexes (d'après BAC S)

infos cours

| 90mn

retour sur le devoir