MATHS-LYCEE.FR exercice corrigé chapitre Maths expertes complexes

PDF reservé aux abonnés

On définit, pour tout entier naturel $n$, les nombres complexes $z$ par :
$\begin{cases} z_{0}= 16\\ z_{n+1}=\dfrac{1 + i}{2}z_{n} \end{cases}$.
On note $r_{n}$ le module du nombre complexe $z_{n}$: $ r_{n} =\left|z_{n}\right|$.
Dans le plan muni d'un repère orthonormé direct d'origine O, on considère les points $A_{n}$ d'affixes $z_{n}$.

1. Calculer $z_{1}, z_{2}$ et $z_{3}$.
  
  Aide
  
  On a z_{n+1}=\dfrac{1 + i}{2}z_{n}$ donc $z_1=\dfrac{1 + i}{2}z_{0}$, $z_2=\dfrac{1 + i}{2}z_{1}$
  
  Solution
  
  En prenant successivement $n=0$, $n=1$ puis $n=2$ dans la relation $z_{n+1}=\dfrac{1 + i}{2}z_{n}$ on a:
  $z_1=\dfrac{1 + i}{2}z_{0}$
  $\phantom{z_1}=\dfrac{1 + i}{2}\times 16$
  $\phantom{z_1}=8+8i$
  $z_2=\dfrac{1 + i}{2}z_{1}$
  $\phantom{z_2}=\dfrac{1 + i}{2}(8+8i)$
  $\phantom{z_2}=(1+i)(4+4i)$
  $\phantom{z_2}=4+4i+4i+4i^2$
  $\phantom{z_2}=4+8i-4$
  $\phantom{z_2}=8i$
  $z_3=\dfrac{1 + i}{2}z_{2}$
  $\phantom{z_3}=\dfrac{1 + i}{2}8i$
  $\phantom{z_3}=(1+i)4i$
  $\phantom{z_3}=4i+4i^2$
  $\phantom{z_3}=-4+4i$
  
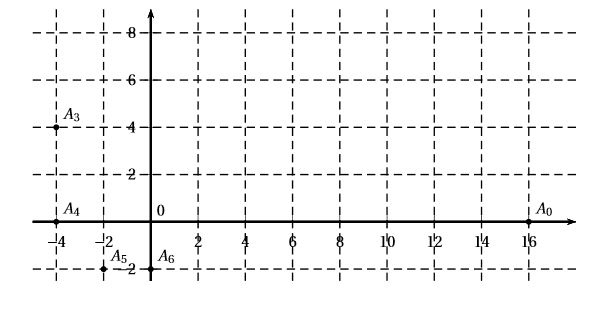
  penser à contrôler les calculs avec la calculatrice (CASIO: OPTION puis CPLX)
2. Placer les points $A_{1}$ et $A_{2}$ sur le graphique ci-dessous.
  
  Rappel de cours
  
  Affixe d'un point et d'un vecteur
  Le complexe $z=x+iy$ ($x$ et $y$ réels) est l'affixe du point $M(x;y)$. l Avec $\overrightarrow{u}(a;b)$, le complexe $u=a+ib$ est l'affixe du vecteur $\overrightarrow{u}$.
  
  Solution
  
  $A_1$ a pour affixe $8+8i$ donc $A_1(8;8)$.
  $A_2$ a pour affixe $8i$ donc $A_2(0;8)$.
  $A_3$ a pour affixe $4+4i$ donc $A_3(-4;4)$.
3. Écrire le nombre complexe $\dfrac{1 + i}{2}$ sous forme trigonométrique.
  
  Rappel de cours
  
  Forme trigonométrique
  Soit $z=x+iY$ un complexe.
  Le module de $z$ noté $|z|$ est $|z|=OM=\sqrt{x^2+y^2}$.
  Si $z\neq 0$ l'argument de $z$ noté $arg(z)$ est une mesure en radians de l'angle $(\overrightarrow{i};\overrightarrow{OM})$}
  On a alors $x=|z|cos(arg(z))$ et $y=|z|sin(arg(z))$ soit $z=|z|(cos(arg(z)+isin(arg(z))$
  Cette forme est appelée forme trigonométrique} de $z$.
  
  Solution
  
  $\left|\dfrac{1 + i}{2}\right|=\sqrt{\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{2}\right)^2}=\sqrt{\dfrac{1}{4}+\dfrac{1}{4}}=\sqrt{\dfrac{1}{2}}=\dfrac{1}{\sqrt{2}}$
  $\dfrac{1 + i}{2}=\dfrac{1}{\sqrt{2}}\left(\dfrac{\sqrt{2} +\sqrt{2} i}{2}\right)$
  Si on note $\theta=arg(\left(\dfrac{1+i}{2}\right)$ ($2\pi$), on a:
  $\begin{cases} cos(\theta)=\dfrac{\sqrt{2}}{2}\\ sin(\theta)=\dfrac{\sqrt{2}}{2} \end{cases}$
  donc $\theta=\dfrac{\pi}{4}$ ($2\pi$).
  
  On peut aussi écrire le module sans racine carrée au dénominateur $\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{\sqrt{2}\sqrt{2}}=\dfrac{\sqrt{2}}{2}$
4. Démontrer que le triangle $OA_{0}A_{1}$ est isocèle rectangle en $A_{1}$.
  
  Aide
  
  On peut calculer les modules de $z_0$, $z_1-z_0$ et de $z_1$ puis vèrifier que $OA_1^2+A_0A_1^2=OA_0^2$
  
  Solution
  
  $OA_1=|z_1|=|8+8i|=\sqrt{8^2+8^2}=\sqrt{128}=8\sqrt{2}$
  $A_0A_1=|z_1-z_0|=|8+8i-16|=|-8+8i|=\sqrt{(-8^2+8^2}=\sqrt{128}=8\sqrt{2}$
  $OA_0=|z_0|=|16|=16$
  $OA_1^2+A_0A_1^2=128+128=256$ et $OA_0^2=16^2=256$
  De plus $OA_1=A_0A_1=8\sqrt{2}$
Démontrer que la suite $\left(r_{n}\right)$ est géométrique, de raison $\dfrac{\sqrt{2}}{2}$.
La suite $\left(r_{n}\right)$ est-elle convergente ?
Interpréter géométriquement le résultat précédent.

Rappel de cours

Limite de $q^n$ (suite géométrique)
Si $q > 1 $ alors $\displaystyle \lim_{n \rightarrow +\infty}q^n=+\infty$
Si $-1 < q < 1 $ alors $\displaystyle \lim_{n \rightarrow +\infty}q^n=0$

Aide

Il faut montrer que $r_{n+1}=\dfrac{\sqrt{2}}{2}r_n$
$r_{n+1}=|z_{n+1}|=|\dfrac{1 + i}{2}z_{n}|=\left|\dfrac{1 + i}{2}\right|~|z_{n}|$

Solution

$r_{n+1}=|z_{n+1}|$
$\phantom{r_{n+1}}=\left|\dfrac{1 + i}{2}z_{n}\right|$
$\phantom{r_{n+1}}=\left|\dfrac{1 + i}{2}\right|~|z_{n}|$
$\phantom{r_{n+1}}=\dfrac{1}{\sqrt{2}}|z_{n}|$
$\phantom{r_{n+1}}=\dfrac{\sqrt{2}}{2}r_n$

1. Démontrer que pour tout entier naturel $n$: $A_{n}A_{n+1} = r_{n+1}$.
  
  Aide
  
  L'affixe du vecteur $\overrightarrow{A_{n}A_{n+1}}$ est $z_{n+1}-z_n$
  $A_{n}A_{n+1}=||\overrightarrow{A_{n}A_{n+1}}||=|z_{n+1}-z_n|$
  
  Solution
  
  $A_{n}A_{n+1}=||\overrightarrow{A_{n}A_{n+1}}||$
  $\phantom{A_{n}A_{n+1}}=|z_{n+1}-z_n|$ \textit{ (L'affixe du vecteur $\overrightarrow{A_{n}A_{n+1}}$ est $z_{n+1}-z_n$)}
  $\phantom{A_{n}A_{n+1}}=\left|\dfrac{1 + i}{2}z_{n}-z_n\right|$
  $\phantom{A_{n}A_{n+1}}=\left|\dfrac{-1 + i}{2}z_n\right|$
  $\phantom{A_{n}A_{n+1}}=\left|\dfrac{-1 + i}{2}\right|~|z_n|$
  $\phantom{A_{n}A_{n+1}}=\sqrt{\left(\dfrac{-1}{2}\right)^2+\left(\dfrac{1}{2}\right)^2}~|z_n|$
  $\phantom{A_{n}A_{n+1}}=\sqrt{\dfrac{1}{2}}~r_n$
  $\phantom{A_{n}A_{n+1}}=\dfrac{\sqrt{2}}{2}~r_n$
  $\phantom{A_{n}A_{n+1}}=r_{n+1}$
2. Donner une expression de $L_{n}$ en fonction de $n$.
  
  Rappel de cours
  
  Somme des termes d'une suite géométrique
  La somme $S$ des termes consécutifs d'une suite géométrique de raison $q\neq 1$ est donnée par:
  $S=u_0 \dfrac{1-q^{n+1}}{1-q}$
  Mémo: $S=$premier terme $ \dfrac{1-q^{\text{nombre de termes}}}{1-q}$
  
  Aide
  
  $A_{n}A_{n+1}=r_{n+1}$ donc $A_{0}A_{1}=r_{1}$, $A_{1}A_{2}=r_{2}$...........$A_{n-1}A_{n}=r_{n}$
  
  Solution
  
  $A_{n}A_{n+1}=r_{n+1}$ donc $A_{0}A_{1}=r_{1}$ (avec $n=0$), $A_{1}A_{2}=r_{2}$ (avec $n=1$)...........$A_{n-1}A_{n}=r_{n}$ (avec $n-1$)
  $L_{n} = \displaystyle\sum_{i=0}^{n-1} A_{i}A_{i+1} = A_{0}A_{1} + A_{1}A_{2} + \ldots + A_{n-1}A_{n}$
  $\phantom{L_{n}}=r_1+r_2+......+r_n$
  $\phantom{L_{n}}=r_1\dfrac{1-q^n}{1-q}$ avec $q=\dfrac{\sqrt{2}}{2}$ et $r_1=|z_1|=8\sqrt{2}$
  $\phantom{L_{n}}=r_1\dfrac{1-\left(\dfrac{\sqrt{2}}{2}\right)^n}{1-\dfrac{\sqrt{2}}{2}}$
  $\phantom{L_{n}}=8\sqrt{2}\dfrac{1-\left(\dfrac{\sqrt{2}}{2}\right)^n}{1-\dfrac{\sqrt{2}}{2}}$
  $\phantom{L_{n}}=8\sqrt{2}\dfrac{1-\left(\dfrac{\sqrt{2}}{2}\right)^n}{\dfrac{2-\sqrt{2}}{2}}$
  $\phantom{L_{n}}=8\sqrt{2}\times \dfrac{2}{2-\sqrt{2}}\times \left(1-\left(\dfrac{\sqrt{2}}{2}\right)^n\right)$
  $\phantom{L_{n}}=\dfrac{16\sqrt{2}}{2-\sqrt{2}}\left(1-\left(\dfrac{\sqrt{2}}{2}\right)^n\right)$
3. Déterminer la limite éventuelle de la suite $\left(L_{n}\right)$.
  
  Aide
  
  Il faut déterminer la limite de $\displaystyle \lim_{n \rightarrow +\infty}\left(\dfrac{\sqrt{2}}{2}\right)^n\right)$
  
  Solution
  
  On a $\dfrac{\sqrt{2}}{2}\in ]0;1[$ donc $\displaystyle \lim_{n \rightarrow +\infty}\left(\dfrac{\sqrt{2}}{2}\right)^n=0$
  et par somme $\displaystyle \lim_{n \rightarrow +\infty}1-\left(\dfrac{\sqrt{2}}{2}\right)^n=1$
  puis par produit $\displaystyle \lim_{n \rightarrow +\infty}\dfrac{16\sqrt{2}}{2-\sqrt{2}}\left(1-\left(\dfrac{\sqrt{2}}{2}\right)^n\right)=\dfrac{16\sqrt{2}}{2-\sqrt{2}}$
  
  On peut écrire cette limite sans racine carrée au dénominateur:
  $\dfrac{16\sqrt{2}}{2-\sqrt{2}}=\dfrac{(16\sqrt{2})(2+\sqrt{2})}{(2-\sqrt{2})(2+\sqrt{2})}=\dfrac{32\sqrt{2}+32}{2^2-\sqrt{2}^2}=\dfrac{32\sqrt{2}+32}{2}=16+16\sqrt{2}$

devoir nº 1475

Vous pouvez retourner sur le devoir après avoir vu cet exercice

Devoir complet fin de chapitre

- conjugué et forme algébrique d'un quotient
- équations avec des complexes - recherche d'un ensemble de points (modules égaux)
- suites et complexes (d'après BAC S)

infos cours

| 90mn

retour sur le devoir

Affixe d'un point et d'un vecteur

Forme trigonométrique

Limite de $q^n$ (suite géométrique)

Somme des termes d'une suite géométrique

devoir nº 1475

Devoir complet fin de chapitre