1. Home
  2. chapitre 7 Géométrie, vecteurs et coordonnées
  3. exercice corrigé nº378
PDF reservé aux abonnés
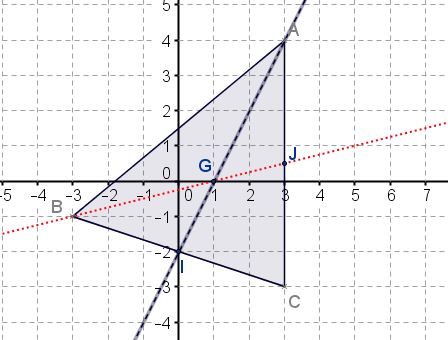
Dans un repère orthonormé, on donne $A(3;4)$, $B(-3;-1)$ et $C(3;-3)$.
penser à contrôler graphiquement les calculs en plaçant les points dans un repère.
  1. Calculer les coordonnées du milieu $I$ de $[BC]$.
    Que représente la droite $(AI)$ pour le triangle $ABC$?

    Rappel de cours

    Coordonnées du milieu d'un segment

    Dans un repère du plan, si on a $A(x_A;y_A)$ et $B(x_B;y_B)$ alors le milieu $I$ de $[AB]$ a pour coordonnées $I\left(\dfrac{x_A+x_B}{2};\dfrac{y_A+y_B}{2}\right)$

    Médianes et centre de gravité

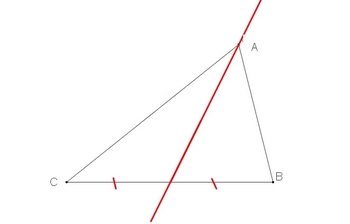
    La médiane issue de $A$ dans un triangle $ABC$ est la droite passant par $A$ et le milieu de $[BC]$ (côté opposé au sommet $A$).

    Centre de gravité
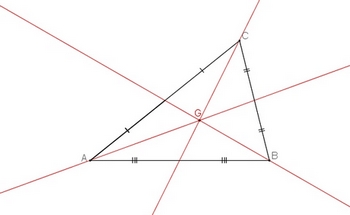
    Le centre de gravité d'un triangle est le point d'intersection des trois médianes.

    Solution

    $\dfrac{x_B+x_C}{2}=\dfrac{-3+3}{2}=0$
    $y_I=\dfrac{y_B+y_C}{2}=\dfrac{-1-3}{2}=-2$

    $(AI)$ passe par le sommet $A$ et le milieu $I$ de $[BC]$
  2. Déterminer les coordonnées du point $G$ tel que $\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AI}$.

    Rappel de cours

    Coordonnées de la somme et du produit par un réel

    Si $\overrightarrow{u}(x;y)$ et $\overrightarrow{w}(x';y')$ alors:
    $\overrightarrow{u}=\overrightarrow{w} \Longleftrightarrow \begin{cases} x=x'\\ y=y' \end{cases}$
    $\overrightarrow{u}+\overrightarrow{w}(x+x';y+y')$
    $k\overrightarrow{u}(kx;ky)$

    Aide

    Il faut calculer les coordonnées du vecteur $\overrightarrow{AI}$

    Solution

    $\begin{cases} x_{\overrightarrow{AI}}=x_I-x_A=0-3=-3\\ y_{\overrightarrow{AI}}=y_I-y_A=-2-4=-6 \end{cases}$
    donc $\overrightarrow{AI}(-3;-6)$
    $\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AI}\Longleftrightarrow \begin{cases} x_G-x_A=\dfrac{2}{3}x_{\overrightarrow{AI}}\\ y_G-y_A=\dfrac{2}{3}y_{\overrightarrow{AI}} \end{cases}$

    $\phantom{\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AI}}\Longleftrightarrow \begin{cases} x_G-3=\dfrac{2}{3}\times (-3)\\ y_G-4=\dfrac{2}{3}\times (-6) \end{cases}$

    $\phantom{\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AI}}\Longleftrightarrow \begin{cases} x_G-3=-2\\ y_G-4=-4 \end{cases}$

    $\phantom{\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AI}}\Longleftrightarrow \begin{cases} x_G=1\\ y_G=0 \end{cases}$
  3. Calculer les coordonnées du milieu $J$ de $[AC]$.
    Montrer que $B$, $J$ et $G$ sont alignés.

    Rappel de cours

    Critère de colinéarité dans un repère

    Dans un repère du plan, $\overrightarrow{u}(x;y)$ et $\overrightarrow{w}(x'y')$ non nuls sont colinéaires si et seulement si $xy'-x'y=0$

    Aide

    Il faut montrer que les vecteurs $\overrightarrow{BJ}$ et $\overrightarrow{BG}$ sont colinéaires.

    Solution

    $x_J=\dfrac{x_A+x_C}{2}=\dfrac{3+3}{2}=3$
    $y_I=\dfrac{y_A+y_C}{2}=\dfrac{4-3}{2}=\dfrac{1}{2}$

    $\begin{cases} x_{\overrightarrow{BJ}}=x_J-x_B=3-(-3)=6\\ y_{\overrightarrow{BJ}}=y_J-y_B=\dfrac{1}{2}-(-1)=\dfrac{3}{2} \end{cases}$
    donc $\overrightarrow{BJ}\left(6;\dfrac{3}{2}\right)$
    $\begin{cases} x_{\overrightarrow{BG}}=x_G-x_B=1-(-3)=4\\ y_{\overrightarrow{BG}}=y_G-y_B=0-(-1)=1 \end{cases}$
    donc $\overrightarrow{BG}\left(4;1\right)$
    $x_{\overrightarrow{BJ}}y_{\overrightarrow{BG}}-y_{\overrightarrow{BJ}}x_{\overrightarrow{BG}}=6\times 1-\dfrac{3}{2}\times 4=6-6=0$
    donc les vecteurs $\overrightarrow{BJ}$ et $\overrightarrow{BG}$ sont colinéaires
  4. Que représente alors le points $G$ pour le triangle $ABC$?

    Aide

    $G$ est le point d'intersection des droites $(AI)$ et $(BJ)$.

    Solution

    $G \in (AI)$ et $G\in (BJ)$ donc $G$ est le point d'intersection des médianes $(AI)$ et $(BJ)$

devoir nº 387


Vous pouvez retourner sur le devoir après avoir vu cet exercice

Vecteurs et vecteurs dans un repère

- somme de deux vecteurs et produit par un réel
- coordonnées d'un vecteur
- alignement

infos cours

| 60mn

retour sur le devoir