- Résoudre $\dfrac{5}{x-6}\leq 3x-2$
Signe de $ax^2+bx+c$
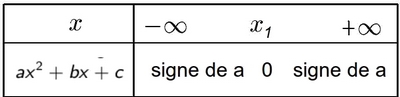
- Cas $\Delta>0$ (deux racines $x_1$ et $x_2$

- Cas $\Delta=0$ (une racine $x_1$)
- Cas $\Delta<0$ (aucune racine)
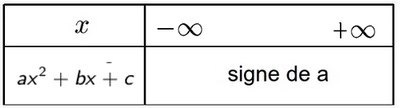 Il faut utiliser un tableau de signes avec un quotient
Il faut utiliser un tableau de signes avec un quotient
Pour obtenir ce quotient, il faut avoir 0 dans le membre de droite et réduire au même dénominateur dans le membre de gaucheIl faut $x-6\neq 0$ soit $x\neq 6$
On résout donc cette inéquation sur $D=\mathbb{R}\setminus \lbrace 6 \rbrace$
$\dfrac{5}{x-6}\leq 3x-2 \Longleftrightarrow \dfrac{5}{x-6}-(3x-2)\leq 0$
$\phantom{\dfrac{5}{x-6}\leq 3x-2} \Longleftrightarrow \dfrac{5}{x-6}-\dfrac{(3x-2)(x-6)}{x-6}\leq 0$
$\phantom{\dfrac{5}{x-6}\leq 3x-2} \Longleftrightarrow \dfrac{5-(3x-2)(x-6)}{x-6}\leq 0$
$\phantom{\dfrac{5}{x-6}\leq 3x-2} \Longleftrightarrow \dfrac{5-(3x^2-18x-2x+12)}{x-6}\leq 0$
$\phantom{\dfrac{5}{x-6}\leq 3x-2} \Longleftrightarrow \dfrac{5-3x^2+18x+2x-12}{x-6}\leq 0$
$\phantom{\dfrac{5}{x-6}\leq 3x-2} \Longleftrightarrow \dfrac{-3x^2+20x-7}{x-6}\leq 0$
Racines de $-3x^2+20x-7$
$\Delta=b^2-4ac=20^2-4\times (-3)\times (-7)=316$
$\Delta>0$ donc il y a deux racines
$x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-20 + \sqrt{316} }{-6 }=\dfrac{-20+2\sqrt{79}}{-6}=\dfrac{-2(10+\sqrt{79})}{-2\times 3}=\dfrac{10-\sqrt{79}}{3}$
et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-20- \sqrt{316} }{-6 }=\dfrac{10+\sqrt{79}}{3}$
On a $x_1\approx 0,4$ et $x_2 \approx 6,3$
Penser à contrôler les racines du numérateur avec le MENU équation de la calculatrice
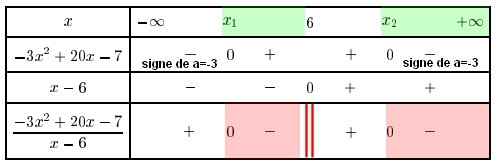
Le quotient doit être positif (zone rouge) pour $x$ appartenant à la zone verte ( valeur interdite!)
Avec une équation, on peut écrire $\dfrac{5}{x-6}= 3x-2=5=(3x-2)(x-6)$
mais on ne peut multiplier par $x-6$ avec une inéquation car selon le signe de $x-6$, l'inégalité change ou pas de sens et on ne connaît pas le signe de $x-6$ - Résoudre $\dfrac{x-1}{x-3}\geq x+2$
Il faut utiliser la même méthode que pour la question 1Il faut $x-3\neq 0$ soit $x\neq 3$
On résout donc cette inéquation sur $D=\mathbb{R}\setminus \lbrace 3 \rbrace$
$\dfrac{x-1}{x-3}\geq x+2 \Longleftrightarrow \dfrac{x-1}{x-3}-( x+2)\geq 0$
$\phantom{\dfrac{x-1}{x-3}\geq x+2} \Longleftrightarrow \dfrac{x-1}{x-3}-\dfrac{( x+2)(x-3)}{x-3}\geq 0$
$\phantom{\dfrac{x-1}{x-3}\geq x+2} \Longleftrightarrow \dfrac{x-1-( x+2)(x-3)}{x-3}\geq 0$
$\phantom{\dfrac{x-1}{x-3}\geq x+2} \Longleftrightarrow \dfrac{x-1-(x^2+2x-3x-6)}{x-3}\geq 0$
$\phantom{\dfrac{x-1}{x-3}\geq x+2} \Longleftrightarrow \dfrac{x-1-x^2-2x+3x+6)}{x-3}\geq 0$
$\phantom{\dfrac{x-1}{x-3}\geq x+2} \Longleftrightarrow \dfrac{-x^2+2x+5}{x-3}\geq 0$
Racines de $-x^2+2x+5$
$\Delta=b^2-4ac=2^2-4\times (-1)\times 5=4+20=24$
$\Delta>0$ donc il y a deux racines
$x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-2 + \sqrt{28} }{-2 }=\dfrac{-2+2\sqrt{6}}{-2}=\dfrac{-2(1-\sqrt{6})}{-2\times 1}=1-\sqrt{6}$
et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-2- \sqrt{24} }{-2 }=1+\sqrt{6}$
On a $x_1\approx -1,4$ et $x_2 \approx 3,4$
Penser à contrôler les racines du numérateur avec le MENU équation de la calculatrice
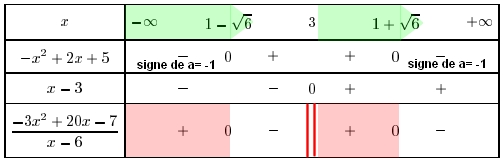
devoir nº 662
Vous pouvez retourner sur le devoir après avoir vu cet exercice
Devoir complet fin de chapitre
- déterminer f à partir du graphique
- inéquations
- polynôme de degré 3
- recettes, coûts et bénéfices
infos cours
| 60mn