1. Home
  2. chapitre 6 Produit scalaire
  3. exercice corrigé nº885
PDF reservé aux abonnés
Le plan est muni d'un repère orthonormé et on donne les points $A(2;1)$, $B(-2;4)$ et $C(1;-3)$.
  1. Faire une figure
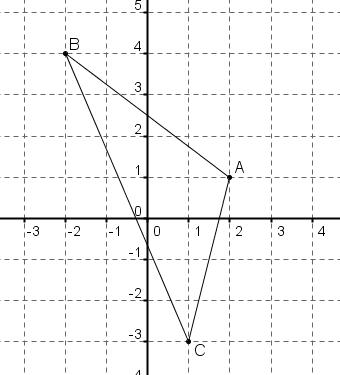
  2. Calculer les coordonnées des vecteurs $ \overrightarrow{AB}$, $ \overrightarrow{AC}$.

    Rappel de cours

    Coordonnées d'un vecteur défini par deux points

    Si $A(x_A;y_A)$ et $B(x_B;y_B)$ alors $\overrightarrow{AB}(x_B-x_A;y_B-y_A)$ (coordonnées du second point $-$ coordonnées du premier point)

    Distance dans un repère

    Dans un repère orthonormé du plan, on a $A(x_A;y_A)$ et $B(x_B;y_B)$,
    $AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$
    Si $\overrightarrow{u}(x;y)$ alors $||\overrightarrow{u}||=\sqrt{x^2+y^2}$

    Solution


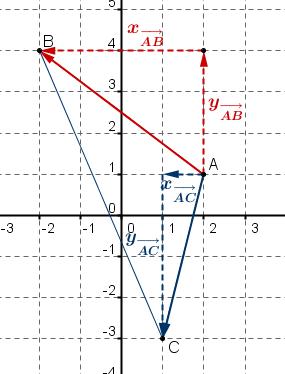
    $\begin{cases} x_{ \overrightarrow{AB}}=x_B-x_A=-2-2=-4 \\ y_{ \overrightarrow{AB}}=y_B-y_A=4-1=3 \end{cases}$
    donc $ \overrightarrow{AB}(-4;3)$

    Vérifier sur la figure le résultat obtenu
    $\begin{cases} x_{ \overrightarrow{AC}}=x_C-x_A=1-2=-1 \\ y_{ \overrightarrow{AC}}=y_C-y_A=-3-1=-4 \end{cases}$
    donc $ \overrightarrow{AC}(-1;-4)$
  3. Calculer $ \overrightarrow{AB}. \overrightarrow{AC}$

    Rappel de cours

    Produit scalaire dans un repère orthonormé

    Dans un repère orthonormé, si $\overrightarrow{u}(x;y)$ et $\overrightarrow{v}(x';y')$ on a:
    $\overrightarrow{u}.\overrightarrow{v}=xx'+yy'$

    Solution


    $ \overrightarrow{AB}. \overrightarrow{AC}=x_{ \overrightarrow{AB}}x_{ \overrightarrow{AC}}+y_{ \overrightarrow{AB}}y_{ \overrightarrow{AC}}$
    $\phantom{ \overrightarrow{AB}. \overrightarrow{AC}}=-4\times (-1)+3\times (-4) $
    $\phantom{ \overrightarrow{AB}. \overrightarrow{AC}}=-8 $
  4. En déduire la mesure de l'angle $\widehat{BAC}$ arrondie au dixième de degré.

    Rappel de cours

    Produit scalaire (définition)

    $\overrightarrow{u}$ et $\overrightarrow{v}$ sont deux vecteurs non nuls tels que $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$, le produit scalaire des deux vecteurs est noté $\overrightarrow{u}.\overrightarrow{v}$,et est le nombre réel défini par:
    $\overrightarrow{u}.\overrightarrow{v}=\mid \mid \overrightarrow{u}\mid \mid\times \mid \mid \overrightarrow{v}\mid \mid \times cos(\widehat{BAC})=AB\times AC\times cos(\widehat{BAC})$

    Aide

    Utiliser le rappel de cours ci-dessus et le résultat de la question 3 pour écrire une équation d'inconnue $\widehat{BAC}$

    Solution

    $ \overrightarrow{AB}. \overrightarrow{AC}=AB\times AC\times cos (\widehat{BAC})= 5\sqrt{17}cos (\widehat{BAC})$
    On a donc $ \overrightarrow{AB}. \overrightarrow{AC}= 5\sqrt{17}cos (\widehat{BAC})=-8$
    $ 5\sqrt{17}cos (\widehat{BAC})=-8$
    $\Longleftrightarrow cos (\widehat{BAC})=\dfrac{-8}{5\sqrt{17}}$
    Avec la calculatrice (réglée en degrés SHIFT MENU), on a donc :
    $\widehat{BAC}=cos^{-1}\left( \dfrac{-8}{5\sqrt{17}}\right)\approx 112,8^o$


    On peut aussi utiliser $ \overrightarrow{AB}. \overrightarrow{AC}=\dfrac{AB^2+AC^2-BC^2}{2}$ mais c'est beaucoup plus long et cela ne présente que peu d'intérêt quand on peut utiliser les coordonnées des vecteurs $ \overrightarrow{AB}$ et $ \overrightarrow{AC}$, ce qui est moins long que le calcul de trois distances

devoir nº 892


Vous pouvez retourner sur le devoir après avoir vu cet exercice

Utiliser les différentes expressions et les propriétés algébriques

- utiliser la bonne expression pour calculer un produit scalaire
- calculs avec le produit scalaire et vecteurs orthogonaux
- calcul d'un angle dans un triangle

infos cours

| 60mn

retour sur le devoir