1. Home
  2. chapitre 6 Produit scalaire
  3. exercice corrigé nº885
PDF reservé aux abonnés
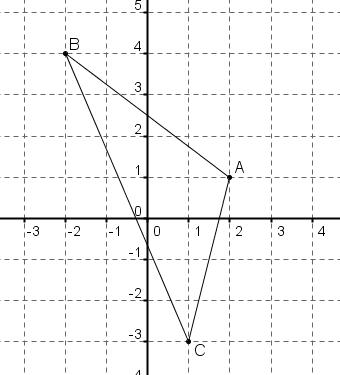
Le plan est muni d'un repère orthonormé et on donne les points $A(2;1)$, $B(-2;4)$ et $C(1;-3)$.
  1. Faire une figure
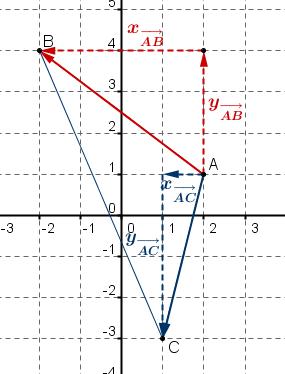
  2. Calculer les coordonnées des vecteurs $ \overrightarrow{AB}$, $ \overrightarrow{AC}$.

    Rappel de cours

    Coordonnées d'un vecteur défini par deux points

    Si $A(x_A;y_A)$ et $B(x_B;y_B)$ alors $\overrightarrow{AB}(x_B-x_A;y_B-y_A)$ (coordonnées du second point $-$ coordonnées du premier point)

    Distance dans un repère

    Dans un repère orthonormé du plan, on a $A(x_A;y_A)$ et $B(x_B;y_B)$,
    $AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$
    Si $\overrightarrow{u}(x;y)$ alors $||\overrightarrow{u}||=\sqrt{x^2+y^2}$

    Solution


    $\begin{cases} x_{ \overrightarrow{AB}}=x_B-x_A=-2-2=-4 \\ y_{ \overrightarrow{AB}}=y_B-y_A=4-1=3 \end{cases}$
    donc $ \overrightarrow{AB}(-4;3)$

    Vérifier sur la figure le résultat obtenu
    $\begin{cases} x_{ \overrightarrow{AC}}=x_C-x_A=1-2=-1 \\ y_{ \overrightarrow{AC}}=y_C-y_A=-3-1=-4 \end{cases}$
    donc $ \overrightarrow{AC}(-1;-4)$
  3. Calculer $ \overrightarrow{AB}. \overrightarrow{AC}$

    Rappel de cours

    Produit scalaire dans un repère orthonormé

    Dans un repère orthonormé, si $\overrightarrow{u}(x;y)$ et $\overrightarrow{v}(x';y')$ on a:
    $\overrightarrow{u}.\overrightarrow{v}=xx'+yy'$

    Solution


    $ \overrightarrow{AB}. \overrightarrow{AC}=x_{ \overrightarrow{AB}}x_{ \overrightarrow{AC}}+y_{ \overrightarrow{AB}}y_{ \overrightarrow{AC}}$
    $\phantom{ \overrightarrow{AB}. \overrightarrow{AC}}=-4\times (-1)+3\times (-4) $
    $\phantom{ \overrightarrow{AB}. \overrightarrow{AC}}=-8 $
  4. En déduire la mesure de l'angle $\widehat{BAC}$ arrondie au dixième de degré.

    Rappel de cours

    Produit scalaire (définition)

    $\overrightarrow{u}$ et $\overrightarrow{v}$ sont deux vecteurs non nuls tels que $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$, le produit scalaire des deux vecteurs est noté $\overrightarrow{u}.\overrightarrow{v}$,et est le nombre réel défini par:
    $\overrightarrow{u}.\overrightarrow{v}=\mid \mid \overrightarrow{u}\mid \mid\times \mid \mid \overrightarrow{v}\mid \mid \times cos(\widehat{BAC})=AB\times AC\times cos(\widehat{BAC})$

    Aide

    Utiliser le rappel de cours ci-dessus et le résultat de la question 3 pour écrire une équation d'inconnue $\widehat{BAC}$

    Solution

    $ \overrightarrow{AB}. \overrightarrow{AC}=AB\times AC\times cos (\widehat{BAC})= 5\sqrt{17}cos (\widehat{BAC})$
    On a donc $ \overrightarrow{AB}. \overrightarrow{AC}= 5\sqrt{17}cos (\widehat{BAC})=-8$
    $ 5\sqrt{17}cos (\widehat{BAC})=-8$
    $\Longleftrightarrow cos (\widehat{BAC})=\dfrac{-8}{5\sqrt{17}}$
    Avec la calculatrice (réglée en degrés SHIFT MENU), on a donc :
    $\widehat{BAC}=cos^{-1}\left( \dfrac{-8}{5\sqrt{17}}\right)\approx 112,8^o$


    On peut aussi utiliser $ \overrightarrow{AB}. \overrightarrow{AC}=\dfrac{AB^2+AC^2-BC^2}{2}$ mais c'est beaucoup plus long et cela ne présente que peu d'intérêt quand on peut utiliser les coordonnées des vecteurs $ \overrightarrow{AB}$ et $ \overrightarrow{AC}$, ce qui est moins long que le calcul de trois distances

devoir nº 893


Vous pouvez retourner sur le devoir après avoir vu cet exercice

Devoir produit scalaire

- utiliser les différentes expressions du produit scalaire
- calculs avec le produit scalaire
- problème ouvert

infos cours

| 60mn

retour sur le devoir