Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
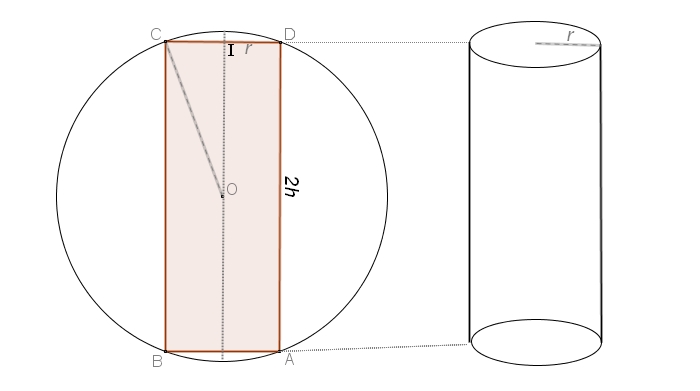
On veut placer une poubelle cylindrique(en rouge) dans une sphère de 1,2 mètre de diamètre.
On note $r$ le rayon du cylindre et $2h$ sa hauteur, ces longueurs étant exprimées en dm.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
On note $r$ le rayon du cylindre et $2h$ sa hauteur, ces longueurs étant exprimées en dm.

- Exprimer $r$ en fonction de $h$.
On peut utiliser le triangle $OCI$ rectangle en $C$On peut utiliser le triangle $OIC$ (ou bien $ACD$) rectangle en $C$.
On a alors $OI=h$.
Le diamètre de la sphère est de 1,2 m
donc le rayon de la sphère est $0,6$ mètre et $OC=6$ dm.
$OC^2=OI^2+IC^2$ soit $6^2=h^2+r^2$
donc $r^2=36-h^2$
- En déduire le volume, en cm$^3$, de la poubelle en fonction de $h$.
- Déterminer alors le rayon et la hauteur du cylindre pour que le volume soit maximal.
Calculer, au dm$^3$ près, le volume maximal de la poubelle.Si on pose $V(h)=2\pi (36h-h^3)$, il faut déterminer le maximum de $V(h)$
Pour déterminer le maximum, il faut dresser le tableau de variation et donc étudier le signe de la dérivée.La sphère a un diamètre de 1,2m$=$12dm.
$0\leq 2h \leq 12 \Longleftrightarrow 0\leq h\leq 6$
On a étudie donc la fonction $V(h)=2\pi (36h-h^3)$ sur $[0;6]$.
$V$ est dérivable sur $[0;6]$ (somme de fonctions dérivables)
$V'(h)=2\pi (36-3h^2)$
Racines de $36-3h^2$:
$36-3h^2=0\Longleftrightarrow 36=3h^2$
$\phantom{36-3h^2=0}\Longleftrightarrow 12=h^2$
$\phantom{36-3h^2=0}\Longleftrightarrow h=\sqrt{12}$ ou $h=-\sqrt{12}$
$\phantom{36-3h^2=0}\Longleftrightarrow h=2\sqrt{3}$ ou $h=-2\sqrt{3}$
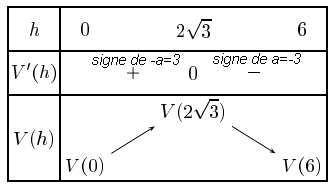
avec $V(0)=2\pi (36\times 0-0^3)=0$
et $V(6)=2\pi (36\times 6-6^3)=0$
$V(2\sqrt{3})=2\pi (36\times 2\sqrt{3}-2^3\sqrt{3}^3)$
$\phantom{V(2\sqrt{3})}=2\pi (72\sqrt{3}-8\times \sqrt{3}^2\times \sqrt{3})$
$\phantom{V(2\sqrt{3})}=2\pi (72\sqrt{3}-24\sqrt{3})$
$\phantom{V(2\sqrt{3})}=2\pi \times 48\sqrt{3}$
$\phantom{V(2\sqrt{3})}=96\pi \sqrt{3}$
Le volume maximum est atteint pour $h=2\sqrt{3}$ dm.
$r=36-h^2=36-12=24$ dm
Le volume maximum est alors $V(2\sqrt{3})=96\pi \sqrt{3}\approx 522$ dm$^3$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
nº787 Recherche d'un minimum
| 10-15mn |
nº786 Recherche d'un minimum
| mn |
nº791 Recherche d'une aire minimale
| 10-15mn |
| 10-15mn |
nº786 Recherche d'un minimum
| mn |
nº791 Recherche d'une aire minimale
| 10-15mn |
