Publications MATHS-LYCEE.FR
Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
$f$ est une fonction définie et dérivable sur $[-3;3]$.
On donne ci-dessous la représentation graphique de la fonction dérivée $f'$ de $f$ définie sur $[-3;3]$.
Dire dans chaque cas si la fonction $f$ est convexe ou concave sur $[-3;3]$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
On donne ci-dessous la représentation graphique de la fonction dérivée $f'$ de $f$ définie sur $[-3;3]$.
Dire dans chaque cas si la fonction $f$ est convexe ou concave sur $[-3;3]$
- fig1
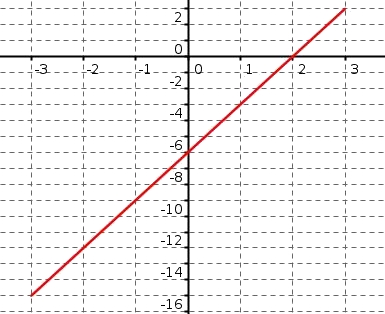
Convexité et variations de la dérivée
Soit $f$ une fonction dérivable sur un intervalle I et $\mathcal{C}_f$ sa courbe représentative.
$f$ est convexe sur I si la courbe $\mathcal{C}_f$ est au-dessus de ses tangentes.
Dans le cas contraire($\mathcal{C}_f$ en-dessous de ses tangentes), $f$ est concave.Pour déterminer si $f$ est convexe ou concave, il faut déterminer le le sens de variation de la fonction $f'$
On peut dresser le tableau de variation de $f'$La fonction $f'$ est croissante sur $[-3;3]$
- fig 2
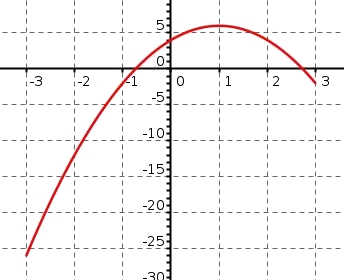Pour déterminer si $f$ est convexe ou concave, il faut déterminer le le sens de variation de la fonction $f'$
On peut dresser le tableau de variation de $f'$La fonction $f'$ est croissante sur $[-3;1[$ et décroissante sur $]1;3]$
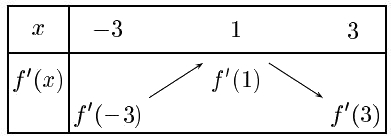
$f$ est convexe sur $[-3;1[$ puis concave sur $]1;3]$
donc la courbe représentative de $f$ admet un point d'inflexion au point de la courbe d'abscisse 1 - fig 3
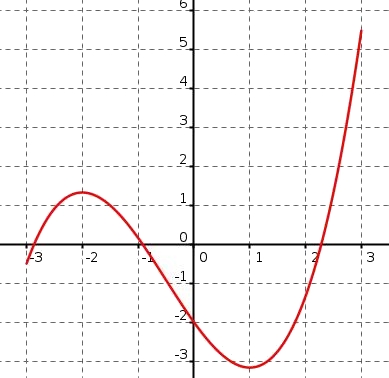Pour déterminer si $f$ est convexe ou concave, il faut déterminer le le sens de variation de la fonction $f'$
On peut dresser le tableau de variation de $f'$La fonction $f'$ est croissante sur $[-3;-2[\cup ]1;3]$ et décroissante sur $]-2;1[$
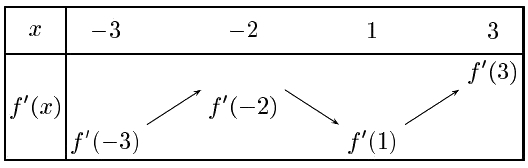
$f$ est convexe sur $[-3;-2[$ puis concave sur $]-2;1[$ puis convexe sur $]1;3]$
donc la courbe représentative de $f$ admet un point d'inflexion au point de la courbe d'abscisse $-2$ et au point de la courbe d'abscisse 1
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Fiche méthode
Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Lien entre dérivée seconde, dérivée et convexité
- convexité et variations de la dérivée
- convexité et signe de la dérivée seconde
infos: | mn |
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.