Publications MATHS-LYCEE.FR

mémo+exercices corrigés+liens vidéos

L'essentiel pour réussir la première en spécialité maths

RÉUSSIR EN MATHS, C'EST POSSIBLE!
Tous les chapitres avec pour chaque notion:
- mémo cours
- exercices corrigés d'application directe
- liens vidéos d'explications.
Il est indispensable de maîtriser parfaitement les notions de base et leur application directe pour pourvoir ensuite les utiliser dans la résolution de problèmes plus complexes.

Plus d'infos
  1. spécialité maths terminale
  2. chapitre 9 Coordonnées dans l'espace
  3. exercice corrigé nº1375

Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!

Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.
*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
PDF reservé aux abonnés
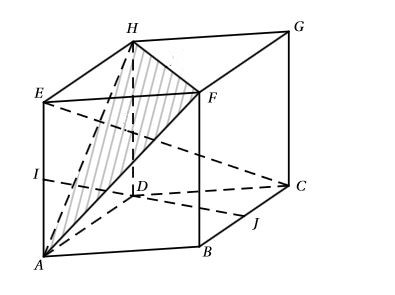
Description de la figure dans l'espace muni du repère orthonormé $\left(A;\overrightarrow{AB};\overrightarrow{AD};\overrightarrow{AE}\right)$
$ABCDEFGH$ désigne un cube de côté 1.
On appelle $\mathcal{P}$ le plan $(AFH)$.
Le point $I$ est le milieu du segment $[AE]$,
le point $J$ est le milieu du segment $[BC]$,
  1. Donner (sans justifier) les coordonnées des sommets du cube dans le repère $\left(A;\overrightarrow{AB};\overrightarrow{AD};\overrightarrow{AE}\right)$.

    Aide

    $(AB)$ est l'axe des abscisses et $B(1;0;0)$...

    Solution

    $A$ est l'origine du repère donc $A(0;0;0)$.
    $(AB)$ défini l'axe des abscisses et $[AB]$ est l'unité de longueur donc $B(1;0;0)$.
    De même, $D(0;1;0)$ et $E(0;0;1)$.
    $C(1;1;0)$, $F(1;0;1)$, $G(1;1;1)$ et $H(0;1;1)$.
  2. Calculer les coordonnées de $I$ et de $J$ et en déduire que les $(IJ)$ et $(EC)$ sont strictement parallèles.

    Rappel de cours

    Coordonnées du milieu

    L'espace est muni d'un repère quelconque.
    Soit $A(x_A;y_A;z_A)$ et $B(x_B;y_B;z_B)$ Le milieu $I$ de $[AB]$ a pour coordonnées $\left(\dfrac{x_A+x_B}{2};\dfrac{y_A+y_B}{2};\dfrac{z_A+z_B}{2}\right)$

    Solution

    $\begin{cases} x_I=\dfrac{x_A+x_E}{2}=\dfrac{0+0}{2}=0\\ y_I=\dfrac{y_A+y_E}{2}=\dfrac{0+0}{2}=0\\ z_I=\dfrac{z_A+z_E}{2}=\dfrac{0+1}{2}=\dfrac{1}{2} \end{cases}$

    $\begin{cases} x_J=\dfrac{x_B+x_C}{2}=\dfrac{1+1}{2}=1\\ y_J=\dfrac{y_B+y_C}{2}=\dfrac{0+1}{2}=\dfrac{1}{2}\\ z_J=\dfrac{z_B+z_C}{2}=\dfrac{0+0}{2}=0 \end{cases}$

    $\begin{cases} x_{\overrightarrow{IJ}}=x_J-x_I=1-0=1\\ y_{\overrightarrow{IJ}}=y_J-y_I=\dfrac{1}{2}\\ z_{\overrightarrow{IJ}}=z_J-z_I=-\dfrac{1}{2} \end{cases}$
    donc $\overrightarrow{IJ}\begin{pmatrix} 1\\ \dfrac{1}{2}\\ -\dfrac{1}{2} \end{pmatrix} $
    et $\overrightarrow{EC}\begin{pmatrix} 1\\ 1\\ -1 \end{pmatrix}$
    $x_{\overrightarrow{IJ}}=1=x_{\overrightarrow{EC}}$
    et $2y_{\overrightarrow{IJ}}=2\times \dfrac{1}{2}=1=y_{\overrightarrow{EC}}$
    donc il n'existe pas de réel $k$ tel que $k\overrightarrow{IJ}=\overrightarrow{EC}$ ñ donc les vecteurs $\overrightarrow{IJ}$ et $\overrightarrow{EC}$ ne sont pas colinéaires
  3. Les droites $(IJ)$ et $(EC)$ sont-elles coplanaires?

    Aide

    $I$ appartient au plan $(ECA)$...

    Solution

    $I$ appartient au plan $(ECA)$ donc si $(IJ)$ et $(EC)$ étaient coplanaires alors le point $J$ appartiendrait au plan $(ECA)$ or $J\notin (ECA)$
  4. Les droites $(AF)$ et $(BG)$ sont-elles orthogonales?

    Rappel de cours

    Produit scalaire dans un repère orthonormé de l'espace

    Dans un repère orthonormé de l'espace, on a les vecteurs $\overrightarrow{u}\begin{pmatrix} x\\ y\\ z \end{pmatrix}$ et $\overrightarrow{v}\begin{pmatrix} x'\\ y'\\ z' \end{pmatrix}$.
    $\overrightarrow{u}.\overrightarrow{v}=xx'+yy'+zz'$

    Orthogonalité et produit scalaire

    Pour tous vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$, on a:
    $\overrightarrow{u}.\overrightarrow{v}=0 \Longleftrightarrow \overrightarrow{u}=\overrightarrow{0}$ ou $\overrightarrow{v}=\overrightarrow{0}$ ou $\overrightarrow{u}$ et $\overrightarrow{v}$ sont orthogonaux.

    Solution

    $\overrightarrow{AF}\begin{pmatrix} 1\\ 0\\ 1 \end{pmatrix}$ et $\overrightarrow{BG}\begin{pmatrix} 0\\ 1\\ 1 \end{pmatrix}$
    $\overrightarrow{AF}. \overrightarrow{BG}=1\times 0+0\times 1+1\times 1=1$
  5. Ces deux droites $(AF)$ et $(BG)$ sont-elle sécantes?

    Aide

    La droite $(AF)$ coupe le plan $(BCG)$ en $F$

    Solution

    La droite $(AF)$ coupe le plan $(BCG)$ en $F$ car $F$ appartient au plan $(BCG)$.
    or $F\notin (BG)$ dans le plan $(BCG)$
  6. La droite $(EC)$ est-elle perpendiculaire au plan $(AEH)$?

    Rappel de cours

    droite et plan orthogonaux

    Une droite $(d)$ est orthogonale à un plan si et seulement si un vecteur directeur de $(d)$ est orthogonal à deux vecteurs directeurs de du plan.

    Aide

    On peut calculer $\overrightarrow{EC}.\overrightarrow{AF}$ et $\overrightarrow{EC}.\overrightarrow{AH}$

    Solution

    $\overrightarrow{EC}\begin{pmatrix} 1\\ 1\\ -1 \end{pmatrix}$, $\overrightarrow{AF}\begin{pmatrix} 1\\ 0\\ 1 \end{pmatrix}$ et $\overrightarrow{AH}\begin{pmatrix} 0\\ 1\\ 1 \end{pmatrix}$
    $\overrightarrow{EC}.\overrightarrow{AF}=1\times 1+1\times 0+(-1)\times 1=1-1=0$
    et $\overrightarrow{EC}.\overrightarrow{AH}=1\times 0+1\times 1+(-1)\times 1=1-1=0$
    donc le vecteur $\overrightarrow{EC}$ est orthogonal aux vecteurs $\overrightarrow{AF}$ et $\overrightarrow{AH}$
    donc la droite $(EC)$ est orthogonale à deux droites sécantes du plan $(AFH)$

Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)

Fiche méthode


Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.

Equation cartésienne d'un plan

- vecteur normal
- déterminer une équation d'un plan
- position relative d'une droite et d'un plan
- intersection de droites et plans

infos: | 15-20mn |

Afficher la fiche méthode

vidéos semblables


Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
Plan et droite orthogonaux
| 4mn |