Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
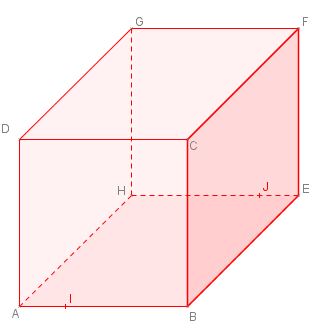
$ABCDEFGH$ est un pavé droit et les points $I$ et $J$ appartiennent respectivement aux segments $[AB]$ et $[HE]$ tel que $(IJ)$ et $(BE)$ ne sont pas parallèles(voir figure ci-dessous).
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)

- Justifier que les droites $(IJ)$ et $(AH)$ sont sécantes en $M$ puis construire le point $M$.
vecteurs coplanaires
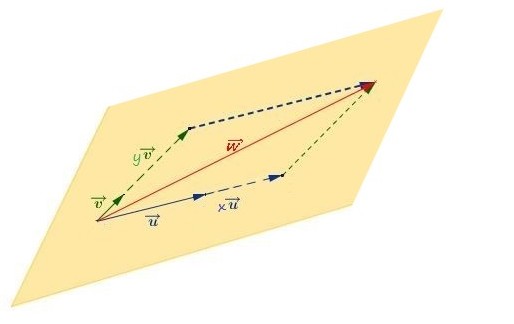
Trois vecteurs $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ non nuls sont coplanaires si les points $A$, $B$, $C$ et $D$ définis par $\overrightarrow{AB}=\overrightarrow{u}$, $\overrightarrow{AC}=\overrightarrow{v}$ et $\overrightarrow{AD} =\overrightarrow{w}$ sont dans un même plan.
 Il faut justifier que les deux droites sont contenues dans un même plan.$I$ et $J$ appartiennent à la face $(ABE)$
Il faut justifier que les deux droites sont contenues dans un même plan.$I$ et $J$ appartiennent à la face $(ABE)$
donc les deux droites $(IJ)$ et $(AH)$ sont donc coplanaires(sont toutes deux inclues dans le plan $(ABE)$)
et d'après l'énoncé $(IJ)$ et $(BE)$ donc $(AH)$ ne sont pas parallèles
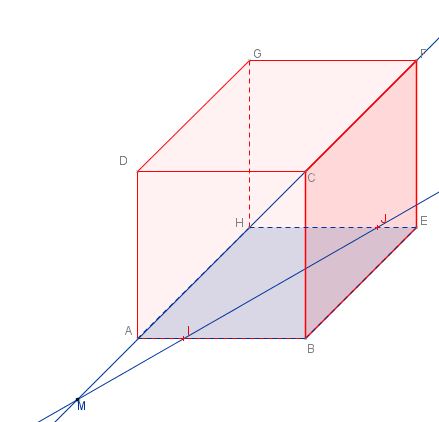
- Construire le point d'intersection $N$ de la droites $(IJ)$ et du plan $(BEF)$.
Il faut utiliser deux droites coplanaires (contenues dans un même plan).$I$ et $J$ appartiennent à la face $(ABE)$
Les deux droites $(IJ)$ et $(BE)$ sont coplanaires(sont toutes deux inclues dans le plan $(ABE)$)
et d'après l'énoncé $(IJ)$ et $(BE)$ ne sont pas parallèles
donc $(IJ)$ et $(BE)$ sont sécantes en $N$.
$N \in (BE)$ donc $N\in (BEF)$.
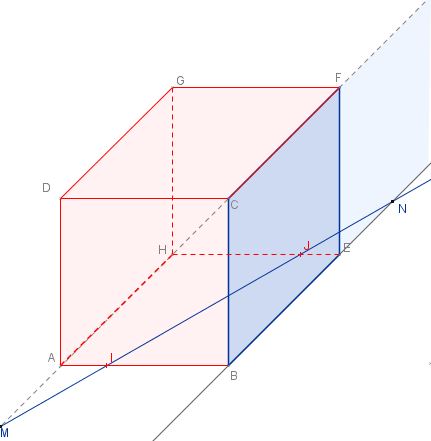
- $K$ est un point du segment $[DC]$ tel que $DK\neq AI$.
Tracer l'intersection du plan $(IJK)$ et du plan $(DCF)$.théorème du toit
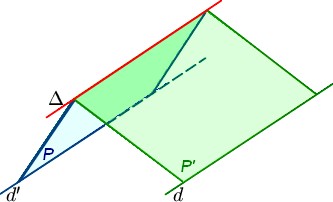
Lorsque deux plans $P$ et $P'$ sont sécants et contiennent respectivement les droites $d$ et $d'$, l'intersection de $P$ et de $P'$ est une droite $\Delta$ parallèle à $d$ et à $d'$.
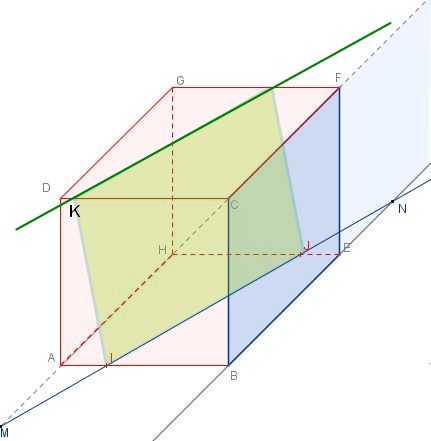
 Il faut utiliser le fait que les plans $(ABE)$ et $(DCF)$ sont parallèles (faces opposées du pavé droit).Les plans $(IJK)$ et $(DCF)$ sont parallèles.
Il faut utiliser le fait que les plans $(ABE)$ et $(DCF)$ sont parallèles (faces opposées du pavé droit).Les plans $(IJK)$ et $(DCF)$ sont parallèles.
L'intersection du plan $(IJK)$ et du plan $(DCF)$ est la droite (en vert) passant par $K$ et parallèle à $(IJ)$ (théorème du toit).
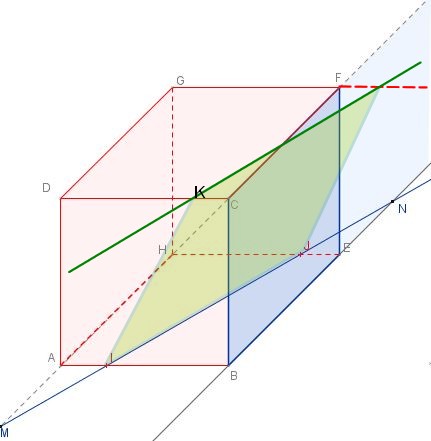
Autre construction possible si $DK > AI$
- En déduire l'intersection des plans $(IJK)$ et $(BEF)$.
Le point $N$ appartient aux plans $(IJK)$ et $(BEF)$
Il faut trouver un second point d'intersection des deux plans en utilisant la droite de la quation précédente et la droite $(CF)$Le point $N$ appartient à la droite $(IJ)$ et au plan $(BCF)$ donc aux plans $(IJK)$ et $(BEF)$
On note $\Delta$ la droite obtenue à la question précédente.
Dans le plan $(DCF)$, les droites $(CF)$ et $\Delta$ son coplanaires et non parallèles (car on sait que $(IJ)$ et $(BF)$ ne sont pas parallèles)
donc $\Delta$ et $(CF)$ sont sécantes en $P$
$P\in (CF)$ donc $P\in (BEF)$
$P\in \Delta$ et $\Delta \subset (IJK)$ donc $P\in (IJK)$
donc $N$ et $P$ sont deux points d'intersection des plans $(IJK)$ et $(BEF)$.
donc la droite $(NP)$(en orange) est la droite d'intersection des plans $(IJK)$ et $BEF)$.
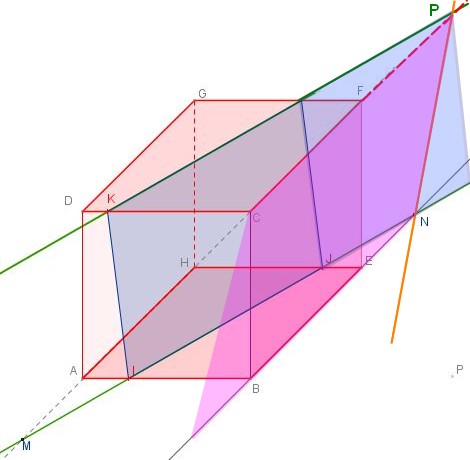
Sans les plans en couleurs, on obtient:
\includegraphics[scale=0.7]{fig7}
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Fiche méthode
Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Intersections de plans et droites
- méthode de construction de l'intersection de deux plans
infos: | 15-20mn |
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
