Publications MATHS-LYCEE.FR

mémo+exercices corrigés+liens vidéos

L'essentiel pour réussir la première en spécialité maths

RÉUSSIR EN MATHS, C'EST POSSIBLE!
Tous les chapitres avec pour chaque notion:
- mémo cours
- exercices corrigés d'application directe
- liens vidéos d'explications.
Il est indispensable de maîtriser parfaitement les notions de base et leur application directe pour pourvoir ensuite les utiliser dans la résolution de problèmes plus complexes.

Plus d'infos
  1. spécialité maths terminale
  2. chapitre 10 Maths expertes complexes
  3. exercice corrigé nº1458

Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!

Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.
*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
PDF reservé aux abonnés
Le plan est muni d'un repère orthonormé d'origine $O$ et on considère les points $A$ et $B$ d'affixes respectives $z_A=1$ et $z_B=-1$.
On considère l'application $f$ qui à tout point $M$ distinct de $B$ associe le point $M'$ d'affixe $z'=f(z)=\dfrac{z-1}{z+1}$.
  1. Déterminer l'ensemble des points invariants par $f$ c'est à dire tels que $f(z)=z$.

    Aide

    On veut résoudre l'équation $f(z)=z$ soit $\dfrac{z-1}{z+1}=z$

    Solution

    $f(z)=z\Longleftrightarrow\dfrac{z -1}{z+1}=z$
    $\phantom{f(z)} \Longleftrightarrow z-1=(z+1)z$
    $\phantom{f(z)} \Longleftrightarrow z^2=-1$
    $\phantom{f(z)} \Longleftrightarrow z=i$ ou $z=-i$
  2. Montrer que pour tout complexe $z\neq -1$ on a $(z'-1)(z+1)=-2$.

    Aide

    Il faut réduire $z'-1=\dfrac{z-1}{z+1}-1$ au même dénominateur

    Solution

    Pour tout complexe $z\neq -1$ on a:
    $(z'-1)(z+1)=\left(\dfrac{z-1}{z+1}-1\right)(z+1)$
    $\phantom{(z'-1)(z+1)}=\left(\dfrac{z-1-(z+1)}{z+1}\right)(z+1)$
    $\phantom{(z'-1)(z+1)}=\left(\dfrac{-2}{z+1}\right)(z+1)$
    $\phantom{(z'-1)(z+1)}=\dfrac{-2(z+1)}{z+1}$
    $\phantom{(z'-1)(z+1)}=-2$
  3. En déduire une relation entre $|z'-1|$ et $|z+1|$ puis entre $arg(z'-1)$ et $arg(z+1)$.

    Aide

    $|-2|=2$ et $arg(-2)=\pi$ ($2\pi$)

    Solution

    $(z'-1)(z+1)=-2$ donc $|(z'-1)(z+1)|=|-2|$
    $|(z'-1)(z+1)|=||z'-1||z+1|$
    donc $|z'-1||z+1|=2$ soit $|z'-1|=\dfrac{2}{|z+1|}$ (rappel: $z\neq -1$ donc $|z+1|\neq 0$)
    $-2=2cos(\pi)$ donc $arg(-2)=\pi$ ($2\pi$)
    et $arg((z'-1)(z+1))=arg(z'-1)+arg(z'+1)$
    donc $arg(z'-1)=\pi-arg(z+1)$ ($2\pi$)
  4. Que peut-on en déduire pour les droites $(AM')$ et $(BM)$?

    Rappel de cours

    Suppression des complexes au dénominateur

    Pour écrire un nombre complexe sans complexes au dénominateur, il faut multiplier le numérateur et le dénominateur par le conjugué du dénominateur.
    En effet $(a+ib)(a-ib)=a^2-iab+iba-i^2b^2=a^2+b^2$
    soit $z\overline{z}=a^2+b^2$
    Exemple:
    $z=\dfrac{2+3i}{1-2i}=\dfrac{(2+3i)(1+2i)}{(1-2i)(1+2i)}=\dfrac{(2+3i)(1+2i)}{1+4}=\dfrac{(2+3i)(1+2i)}{5}$

    Aide

    L'affixe du vecteur $\overrightarrow{AM'}$ est $z'-z_A=z'-1$ et l'affixe du vecteur $\overrightarrow{BM}$ est $z-z_B=z+1$.

    Solution

    $arg(z'-1)=\pi-arg(z+1)$ ($2\pi$) et $z'-1$ est l'affixe du vecteur $\overrightarrow{AM'}$ et $z+1$ est l'affixe du vecteur $\overrightarrow{BM}$
    donc $(\overrightarrow{i};\overrightarrow{AM'})=arg(z'-1)$ ($2\pi$) et $(\overrightarrow{i};\overrightarrow{BM})=arg(z+1)$ ($2\pi$)
    $(\overrightarrow{i};\overrightarrow{AM'})=\pi-(\overrightarrow{i};\overrightarrow{BM})$ ($2\pi$)
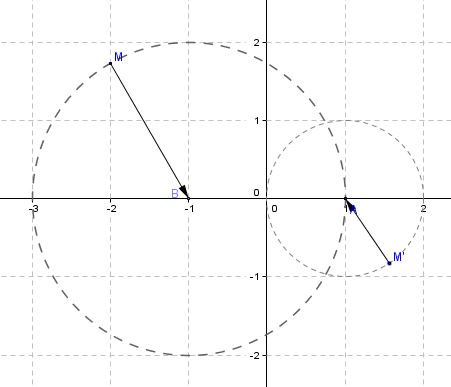
  5. Montrer que si $M$ appartient au cercle de centre $B$ est rayon 2 alors $M'$ appartient au cercle de centre $A$ et rayon 1.

    Aide

    $M$ appartient au cercle de centre $B$ et rayon 2 donc $|z-z_B|=|z+1|=2$

    Solution

    $M$ appartient au cercle de centre $B$ et rayon 2 donc $|z-z_B|=|z+1|=2$ (on a bien $M \neq B$)
    donc $|z'-1|=\dfrac{2}{|z+1|}=\dfrac{2}{2}=1$
    $AM'=|z'-z_A|=|=z'-1|=1$


Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)

vidéos semblables


Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
Recherche d'un ensemble de points
| 4mn |

exercices semblables


Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
nº1457 Recherche d'un ensemble de points (extrait BAC S)
| 15-20mn |
nº1459 ensemble de points
| 8-12mn |