MATHS-LYCEE.FR exercice corrigé chapitre Fonctions de références et étude de fonctions

Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.
*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)

PDF reservé aux abonnés

La fonction $f$ est définie sur $\mathbb{R}$ par $f(x)=x^2$.

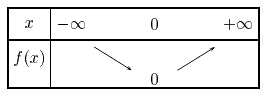
Rappeler le tableau de variation de $f$.

Solution

La fonction carré est décroissante sur $]-\infty;0]$ et croissante sur $[0;+\infty[$.
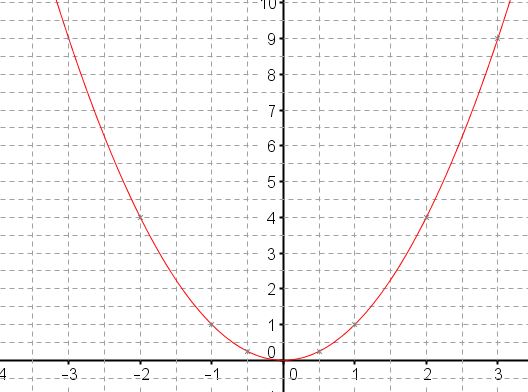
Compléter le tableau de valeurs ci-dessous et tracer la courbe représentative de $f$ dans un repère orthonormal (1cm pour unité sur l'axe des abscisses et 0,5 cm pour unité sur l'axe des ordonnées).

Aide

$(-3)^2=9$

Solution

En plaçant les points de coordonnées $(x;f(x))$ dans le repère ci-dessous, on obtient la courbe représentative de $f$.
Résoudre par le calcul l'équation $f(x)=5$ puis contrôler graphiquement.

Rappel de cours

Calcul d'un (des) antécédent(s)
Pour rechercher les antécédents d'un nombre $\alpha$ par une fonction $f$ définie sur $D_f$, il faut résoudre l'équation $f(x)=\alpha$.
Les valeurs trouvées doivent appartenir à $D_f$.

Aide

Il faut résoudre l'équation $x^2=5$

Solution

$f(x)=5\Longleftrightarrow x^2=5$
$\phantom{x^2=5}\Longleftrightarrow x=\sqrt{5}$ ou $x=-\sqrt{5}$

Graphiquement, les solutions de l'équation $f(x)=5$ sont les abscisses des points d'intersection de la droite d'équation $y=5$ (en vert sur le graphique) et de la courbe

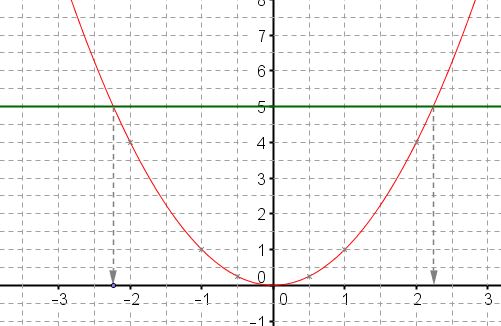
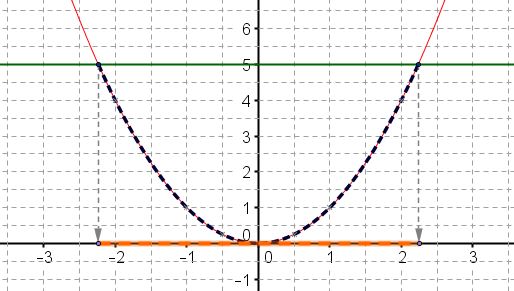
Graphiquement, on obtient deux solutions dont les valeurs sont effectivement proches de $\sqrt{5}\approx 2,2$ et $-\sqrt{5}\approx -2,2$.
En déduire graphiquement les solutions de l'inéquation $f(x)\leq 5$.

Aide

Il faut déterminer les abscisses des points de la courbe dont l'ordonnée est inférieure ou égale à 5

Solution

Graphiquement, les solutions de l'inéquation $f(x)\leq 5$ sont les abscisses (en orange) des points de la courbe (en bleu) situés en dessous de la droite d'équation $y=5$.