Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
On donne ci-dessous sa représentation graphique dans un repère orthogonal.
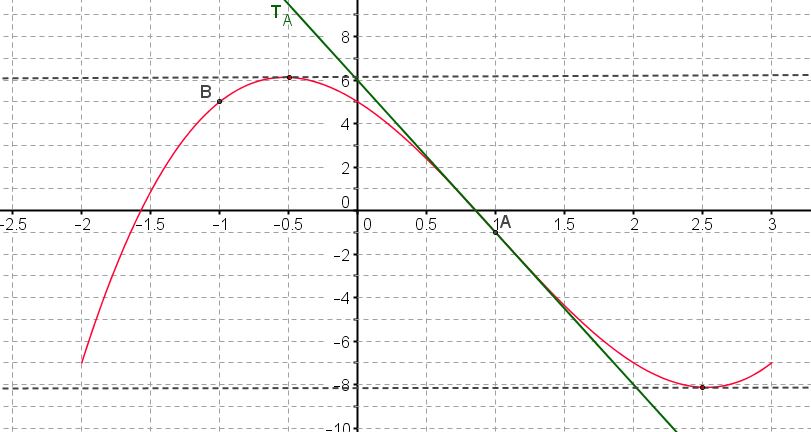
La droite $T_A$ est la tangente à la courbe au point $A$ d'abscisse 1.
Les tangentes aux points d'abscisses $-0,5$ et 2,5 sont parallèles à l'axe des abscisses.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)

La droite $T_A$ est la tangente à la courbe au point $A$ d'abscisse 1.
Les tangentes aux points d'abscisses $-0,5$ et 2,5 sont parallèles à l'axe des abscisses.
- A laide du graphique et des informations données dans l'énoncé, déterminer:
- $f~'(2,5)$ et $f~'(-0,5)$
Équation de la tangente au point d'abscisse $a$
$f$ est une fonction définie et dérivable en $x=a$.
La tangente à $C_f$ en $a$ a pour coefficient directeur $f'(a)$
et pour équation réduite $ y=f'(a)(x-a)+f(a)$}Le coefficient directeur d'une droite parallèle à l'axe des abscisses est nul$f~'(2,5)$ est le coefficient directeur de la tangente à la courbe au point d'abscisse 2,5 et cette tangente est parallèle à l'axe des abscisses
- $f~'(1)$
$f~'(1)$ est le coefficient directeur de la tangente $T_A$ à la courbe au point $A$ d'abscisse 1.
$T_A$ coupe l'axe des ordonnées au point $B(0;6)$.
donc $f~'(1)=\dfrac{y_B-y_A}{x_B-x_A}=\dfrac{6-(-1)}{0-1}=-7$
On peut aussi déterminer le coefficient directeur directement sur le graphique - le signe de $f~'(-1)$
Signe de la dérivée et variations d'une fonction
Soit $f$ une fonction définie et dérivable sur $I$:
$f$ est croissante sur $I$ si et seulement si $f'(x)\geq 0$
$f$ est décroissante sur $I$ si et seulement si $f'(x)\leq 0$Il faut déterminer le sens de variation de $f$ sur un intervalle contenant $-1$Sur l'intervalle $[-2;-0,5]$ la fonction $f$ est strictement croissante donc $f~'(x)$ est de signe positif
- $f~'(2,5)$ et $f~'(-0,5)$
- On donne $f~'(-1)=5$.
Déterminer l'équation réduite de la tangente $T_B$ à la courbe au point $B$ d'abscisse $-1$.Équation de la tangente au point d'abscisse $a$
$f$ est une fonction définie et dérivable en $x=a$.
La tangente à $C_f$ en $a$ a pour coefficient directeur $f'(a)$
et pour équation réduite $ y=f'(a)(x-a)+f(a)$}On donne $f~'(-1)$ et il faut déterminer graphiquement $f(-1)$Le point $B$ a pour ordonnée 5 donc $f(-1)=5$
$T_B~:~~y=f~'(-1)(x-(-1))+f(-1)$ aux signes $-$ successifs $-x_B=-(-1)$
$\phantom{T_B~:~~y}=5(x+1)+5$
$\phantom{T_B~:~~y}=5x+10$
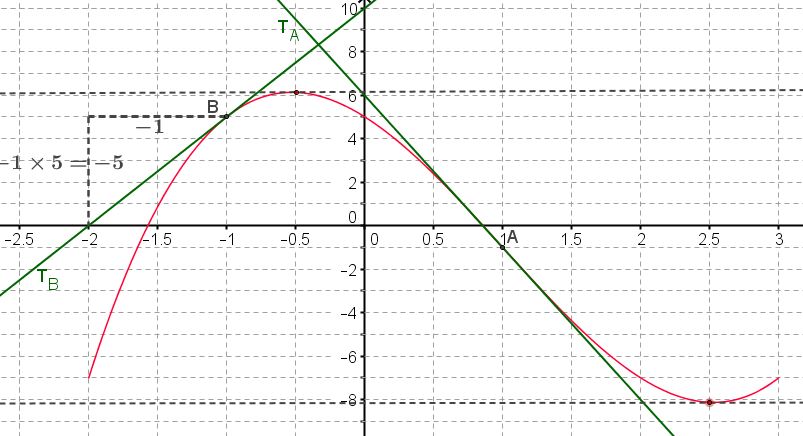
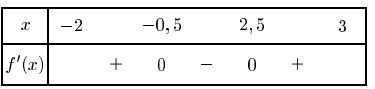
La tangente $T_B$ coupe bien l'axe des ordonnées au point d'ordonnée 10. - Dresser le tableau de signes de $f~'(x)$
Signe de la dérivée et variations d'une fonction
Soit $f$ une fonction définie et dérivable sur $I$:
$f$ est croissante sur $I$ si et seulement si $f'(x)\geq 0$
$f$ est décroissante sur $I$ si et seulement si $f'(x)\leq 0$Il faut déterminer le sens de variation de $f$ pour connaître le signe de sa dérivée$f$ est croissante sur $[-2;-0,5]$ et sur $[2,5;3]$.
on a donc:
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
