Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Le plan est muni d'un repère orthonormé.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
- Le cercle $\mathcal{C}$ admet pour équation $x^2-2x+y^2-4y=45$.
Déterminer le centre $A$ et le rayon $r$ de ce cercle puis le tracer dans un repère orthonormé.(on pourra faire la figure avec GEOGEBRA)Équation d'un cercle
Dans un repère orthonormé, le cercle de centre $C(x_C;y_C)$ et de rayon $r$ a pour équation $(x-x_C)^2+(y-y_C)^2=r^2$$(x-1)^2=x^2-2x+1$
$(y-2)^2=y^2-4y+4$$\phantom{\Longleftrightarrow} x^2-2x+y^2-4y=45$
$\Longleftrightarrow (x-1)^2-1+(y-2)^2-4=45$
$\Longleftrightarrow (x-1)^2+(y-2)^2-5=45$
$\Longleftrightarrow (x-1)^2+(y-2)^2=50$
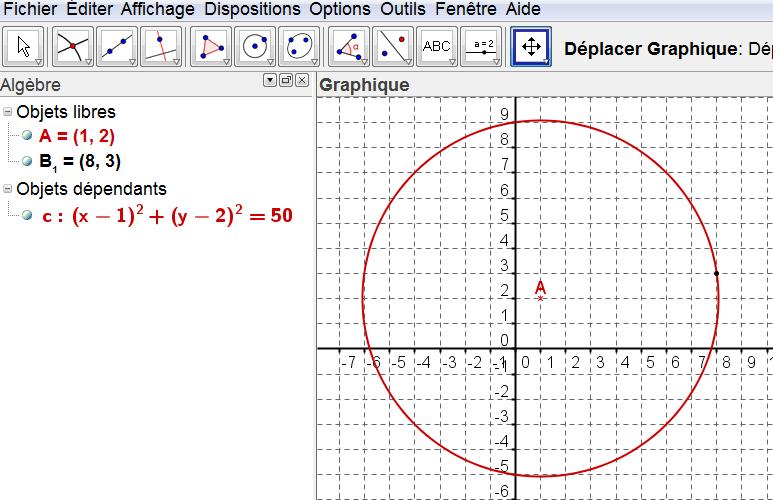
On peut saisir l'équation du cercle donnée dans l'énoncé dans la barre de saisie de GEOGEBRA puis contrôler que le cercle admet bien pour centre $A$
On peut aussi tracer le cercle de centre $A$ et rayon 3 puis vérifier que l'équation affichée est équivalente à celle de l'énoncé. - Déterminer une équation du cercle $\mathcal{C'}$ de centre $B(5;-1)$ et passant par $A$
Distance dans un repère
Dans un repère orthonormé du plan, on a $A(x_A;y_A)$ et $B(x_B;y_B)$,
$AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$
Si $\overrightarrow{u}(x;y)$ alors $||\overrightarrow{u}||=\sqrt{x^2+y^2}$On peut calculer le rayon de ce cercle en calculant la distance $AB$ pour déterminer une équation$AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}=\sqrt{(5-1)^2+(-1-2)^2}=\sqrt{16+9}=5$
donc $\mathcal{C'}$ a pour rayon $5$
et une équation de $\mathcal{C'}$ est donc $(x-5)^2+(y-(-1))^2=5^2$
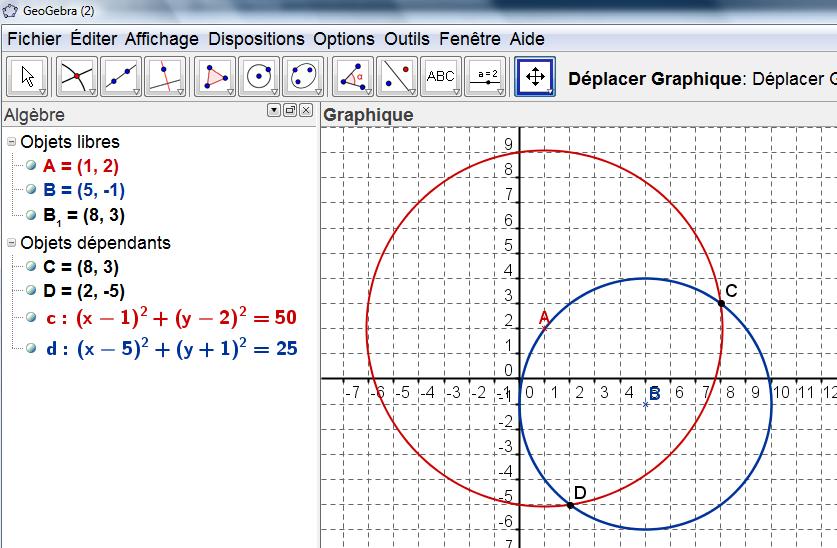
- Déterminer les coordonnées des points d'intersection de $\mathcal{C}$ et de $\mathcal{C'}$ puis contrôler sur la figure la cohérence des résultats obtenus.
Il faut résoudre le système d'équations formé avec les équations des deux cercles
Développer les deux expressions et soustraire les deux lignes
(Avec GEOGEBRA, commande intersection de deux objets puis pointer sur le cercle $\mathcal{C}$ puis $\mathcal{C'}$.Un point $M(x;y)$ appartient au cercle $\mathcal{C}$ et au cercle $\mathcal{C'}$ si ses coordonnées vérifient une équation de chacun des deux cercles, donc il faut résoudre le système d'équations:
$\phantom{\Longleftrightarrow} \begin{cases} (x-1)^2+(y-2)^2=50 \\ (x-5)^2+(y+1)^2=25 \end{cases}$
$\Longleftrightarrow \begin{cases} (x-1)^2+(y-2)^2-50=0 \\ (x-5)^2+(y+1)^2-25=0 \end{cases}$
On développe et on simplifie chaque équation (forme développée)
$\Longleftrightarrow \begin{cases} x^2-2x+y^2-4y-45= 0 \\ x^2-10x+y^2+2y+1 =0 \end{cases}$
On soustrait membre à membre les deux lignes
$\Longleftrightarrow \begin{cases} x^2-2x+y^2-4y-45-(x^2-10x+y^2+2y+1)=0 ~~~~~L_1-L_2 \\ x^2-10x+y^2+2y+1 =0 \end{cases}$
$\Longleftrightarrow \begin{cases} -2x-4y-45+10x-2y-1=0 \\ (x-5)^2+(y+1)^2-25=0 \end{cases}$
$\Longleftrightarrow \begin{cases} 8x-6y-46=0 \\ (x-5)^2+(y+1)^2-25=0 \end{cases}$
$\Longleftrightarrow \begin{cases} y=\dfrac{8x-46}{6} \\ (x-5)^2+(y+1)^2-25=0 \end{cases}$
$\Longleftrightarrow \begin{cases} y=\dfrac{4x-23}{3} \\ (x-5)^2+(\dfrac{4x-23}{3} +1)^2-25=0 ~~~~\text{On remplace }y \text{ par } \dfrac{4x-23}{3} \end{cases}$
$\Longleftrightarrow \begin{cases} y=\dfrac{4x-23}{3} \\ (x-5)^2+(\dfrac{4x-20}{3})^2-25=0 \end{cases}$
$\Longleftrightarrow \begin{cases} y=\dfrac{4x-23}{3} \\ x^2-10x+25+\dfrac{16x^2-160x+400}{9}-25=0 ~~~~\text{on multiplie les deux membres par 9} \end{cases}$
$\Longleftrightarrow \begin{cases} y=\dfrac{4x-23}{3} \\ 9x^2-90x+225+16x^2-160x+400-225=0 \end{cases}$
$\Longleftrightarrow \begin{cases} y=\dfrac{4x-23}{3} \\ 25x^2-250x+400=0 \end{cases}$
$\Longleftrightarrow \begin{cases} y=\dfrac{4x-23}{3} \\ x^2-10x+16=0 \end{cases}$
Recherche des racines de $x^2-10x+16=0 $
$\Delta=b^2-4ac=(-10)^2-4\times 1\times 16=36$ $\Delta>0$
donc il y a deux racines:
$x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{10-6}{2}=2$
et $x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{10+6}{2}=8$
Il y a donc deux points d'intersection $C$ et $D$ de coordonnées:
$x_C=2$ et $y_C=\dfrac{4x_C-23}{3}=\dfrac{-15}{3}=-5$
et $x_D=8$ et $y_D=\dfrac{4x_D-23}{3}=\dfrac{9}{3}=3$
Recherche des racines de $x^2-10x+16=0 $
$\Delta=b^2-4ac=(-10)^2-4\times 1\times 16=36$
$\Delta>0$ donc il y a deux racines:
$x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{10-6}{2}=2$ et $x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{10+6}{2}=8$
Il y a donc deux points d'intersection $C$ et $D$ de coordonnées:
$x_C=2$ et $y_C=\dfrac{4x_C-23}{3}=\dfrac{-15}{3}=-5$
et $x_D=8$ et $y_D=\dfrac{4x_D-23}{3}=\dfrac{9}{3}=3$
Figure:
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Fiche méthode
Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Droites perpendiculaires
- déterminer si deux droites sont perpendiculaires
- déterminer une équation cartésienne d'une perpendiculaire
infos: | mn |
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
