Un sondage a été effectué auprès des anciens élèves d'un lycée quelques années après l'obtention de leur baccalauréat.
Ce sondage révèle que 55% d'entre eux poursuivent leurs études à la faculté, 10% ont intégré une école d'ingénieur et le pourcentage restant est sur le marché du travail (en activité ou en recherche d'emploi).
Ce sondage révèle aussi que :
45% des anciens élèves qui poursuivent leurs études à la faculté ont fait le choix de vivre en colocation.
30% des anciens élèves qui ont intégré une école d'ingénieur ont fait le choix de vivre en colocation.
15% des anciens élèves sur le marché du travail ont fait le choix de vivre en colocation.
On interroge au hasard un ancien élève du lycée et on note :
$F$ l'évènement : "l'ancien élève poursuit ses études à la faculté";
$I$ l'évènement : " l'ancien élève a intégré une école d'ingénieur " ;
$T$ l'évènement : " l'ancien élève est sur le marché du travail" ;
$C$ l'évènement : " l'ancien élève vit en colocation ".
- Construire un arbre pondéré décrivant la situation.
Arbre pondéré
Probabilités sur un arbre pondéré:
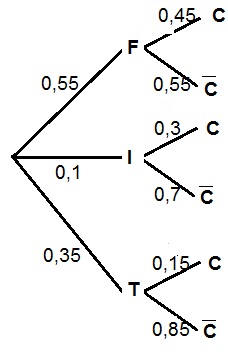
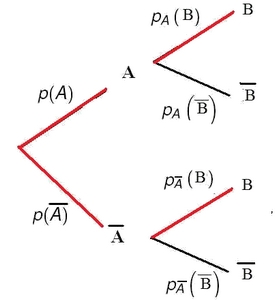 Placer les probabilités non conditionnelles au premier nievau de l'arbre, soit $p(F)$, $P(I)$ et $p(T)55% des élèves poursuivent leurs études à la faculté donc $p(F)=0,55$
Placer les probabilités non conditionnelles au premier nievau de l'arbre, soit $p(F)$, $P(I)$ et $p(T)55% des élèves poursuivent leurs études à la faculté donc $p(F)=0,55$
10% des élèves poursuivent des études d'ingénieur donc $p(I)=0,1$
45% des anciens élèves qui poursuivent leurs études à la faculté ont fait le choix de vivre en colocation donc $p_F(C)=0,45$.
30% des anciens élèves qui ont intégré une école d'ingénieur ont fait le choix de vivre en colocation donc $p_I(C)=0,3$
15% des anciens élèves sur le marché du travail ont fait le choix de vivre en colocation donc $p_T(C)=0,15$
-
- Exprimer à laide d'une phrase l'évènement $F \cap C$ puis calculer la valeur exacte de sa probabilité.
Probabilité de l'événement $A\cap B$
Soient $A$ et $B$ deux événements avec $p(A)\neq 0$, on a
$p(A\cap B)=p(A)\times p_A(B)$$F\cap C$ se lit événement $F$ et $C$ réalisés$F \cap C$ signifie que l'étudiant est en faculté et en colocation
$p(F\cap C)=p(F) p_F(C)=0,55 \times 0,45=0,2475$
- Montrer que la probabilité de l'évènement $C$ est égale à $0,33$.
Arbre pondéré
Probabilités sur un arbre pondéré:
 Il faut calculer $p(C)$ en utilisant la formule des probabilités totales et/ou l'arbre en identifiant les parcours menant à l'événement $C$.$F$,$I$ et $T$ sont disjoints deux à deux et $F\cap I\cap T=\Omega$
Il faut calculer $p(C)$ en utilisant la formule des probabilités totales et/ou l'arbre en identifiant les parcours menant à l'événement $C$.$F$,$I$ et $T$ sont disjoints deux à deux et $F\cap I\cap T=\Omega$
donc $F$, $T$ et $I$ forment une partition de l'univers
donc en utilisant la formule des probabilités totales, on a:
$p(C)=p(F\cap C)+p(I\cap C)+p(T\cap C)$
$\phantom{p(C)}=0,2475+p(I)p_I(C)+p(T) p_T(C)$
$\phantom{p(C)}=0,2475+0,1 \times 0,3+0,35\times 0,15$
$\phantom{p(C)}=0,33$
- Exprimer à laide d'une phrase l'évènement $F \cap C$ puis calculer la valeur exacte de sa probabilité.
- Un ancien élève vit en colocation.
Calculer la probabilité qu'il poursuive ses études à la faculté.Probabilité conditionnelle
Soient $A$ et $B$ deux événements avec $p(A)\neq 0$.
La probabilité que l'événement $B$ soit réalisé sachant que l'événement $B$ est réalisé se note $p_A(B)$
et on a $p_A(B)=\dfrac{p(A\cap B)}{p(A)}$.On veut calculer $p_C(F)$La probabilité que l'élève poursuive ses études à la faculté sachant qu'il est en colocation se note $p_C(F)$.
$p_C(F)=\dfrac{p(C\cap F)}{p(C)}=\dfrac{0,2475}{0,33}=0,75$
- Dans cette question, toute trace de recherche, même incomplète, ou d'initiative, même non fructueuse, sera prise en compte dans l'évaluation.
Le responsable du sondage affirme : " Plus de la moitié des élèves n'ayant pas fait le choix de la colocation poursuivent des études".
Cette affirmation est-elle correcte ? Justifier.On veut calculer $p_{\overline{C}}(\overline{T})$La probabilité de l'événement "l'élève poursuit ses études sachant qu'il n'a pas fait le choix de la colocation" se note $p_{\overline{C}}(\overline{T})$.
$p_{\overline{C}}(\overline{T})=\dfrac{p(\overline{C}\cap \overline{T})}{p(\overline{C})}$.
$p(\overline{C}\cap \overline{T})=p(F\cap \overline{C})+p(I\cap \overline{C})=0,55\times 0,55+0,1\times 0,7=0,3725$
$p(\overline{C})=1-p(C)=1-0,33=0,67$
donc $p_{\overline{C}}(\overline{T})=\dfrac{p(\overline{C}\cap \overline{T})}{p(\overline{C})}=\dfrac{0,3725}{0,67}\approx 0,56$.
- On interroge au hasard trois anciens élèves. On suppose que le nombre d'anciens élèves est suffisamment important pour considérer que ce choix est fait de manière indépendante.
- Construire un arbre pondéré illustrant la situation
Les expériences sont indépendantesOn considère l'épreuve "On choisit un élève au hasard " et cette expérience a deux issues possibles:
soit l'élève est en colocation avec $p(C)=0,33$ soit il ne l'est pas avec $p(\overline{C})=1-0,33=0,67$
On répète 3 fois successivement cette expérience aléatoire et ces trois épreuves sont indépendantes.
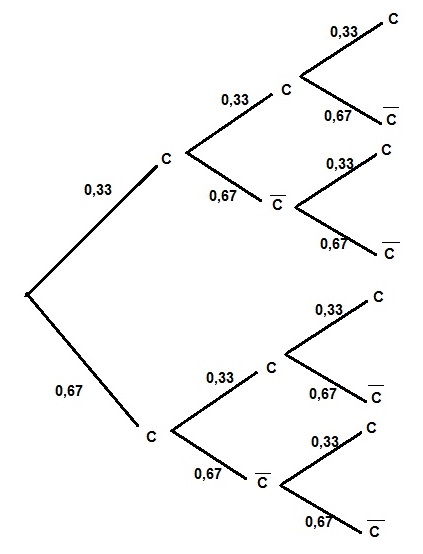
- Calculer la probabilité pour qu'au moins un des anciens élèves vive en colocation. On arrondira le résultat à $10^{-2}$ près.
Au moins un des trois est le contraire de aucun n'est en colocationSi on note $X$ la variable aléatoire donnant le nombre d'élèves en colocation parmi les 3.
On veut qu'au moins un des trois soit en colocation donc $X\geq 1$.
$p(X \geq 1)=p(X=1)+p(X=2)+p(X=3)=1-p(X=0)$
$p(X=0)=p(\overline{C})^3=0,67^3$
donc $p(X\geq 1)=1-p(X=0)=1-0,67^3\approx 0,6992 \approx 0,7$ en arrondissant à $10^{-2}$ soit $0,01$.
- Construire un arbre pondéré illustrant la situation
devoir nº 975
Vous pouvez retourner sur le devoir après avoir vu cet exercice
Devoir complet fin de chapitre probabilités
- arbre pondéré
- probabilités conditionnelles
- probabilités totales
- loi de probabilités et espérance
infos cours
| 60mn