Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Donner l'ensemble de définition de $f$ puis compléter la représentation graphique des fonctions suivantes:
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
- $f$ est une fonction paire.
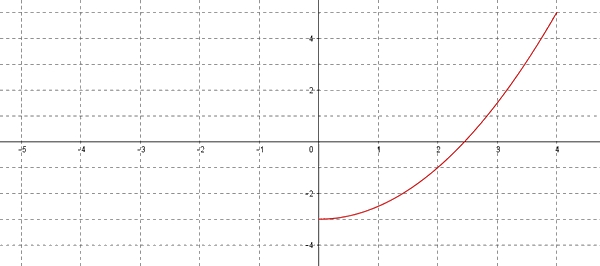
Fonction paire
Une fonction $f$ définie sur $\mathbb{R}$ est paire si pour tout réel $x$ de $D$ on a:
$\begin{cases} -x\in D\\ f(-x)=f(x) \end{cases}$
La représentation graphique de $f$ est alors symétrique par rapport à l'axe des ordonnées.
Remarque: pour tout réel $x\in D$ on a $-x\in D$ signifie que l'ensemble de définition est symétrique par rapport au zéro.
Par exemple si $D=[-3;5]$ la fonction $f$ ne peut pas être paire.Déterminer d'abord l'ensemble de définition de $f$
La courbe est symétrique par rapport à l'axe des ordonnéesPour que l'axe des ordonnées soit un axe de symétrie, on doit avoir $D_f=[-4;4]$
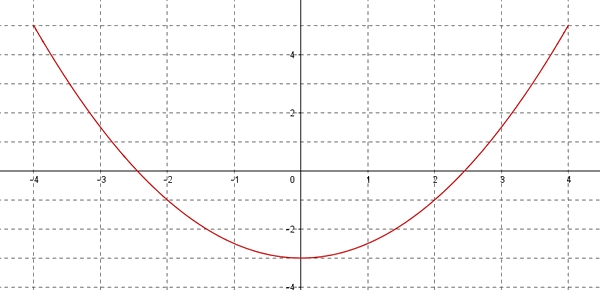
- $f$ est une fonction impaire.
Fonction impaire
Une fonction $f$ définie sur $\mathbb{R}$ est impaire si pour tout réel $x$ de $D$ on a:
$\begin{cases} -x\in D\\ f(-x)=-f(x) \end{cases}$
La représentation graphique de $f$ est alors symétrique par rapport à l'origine du repère.
Remarque: pour tout réel $x\in D$ on a $-x\in D$ signifie que l'ensemble de définition est symétrique par rapport au zéro.
Par exemple si $D=[-3;5]$ la fonction $f$ ne peut pas être impaire.Déterminer d'abord l'ensemble de définition de $f$
La courbe est symétrique par rapport à l'origine du repèrePour que l'origine du repère soit un centre de symétrie, on doit avoir $D_f=[-4;4]$
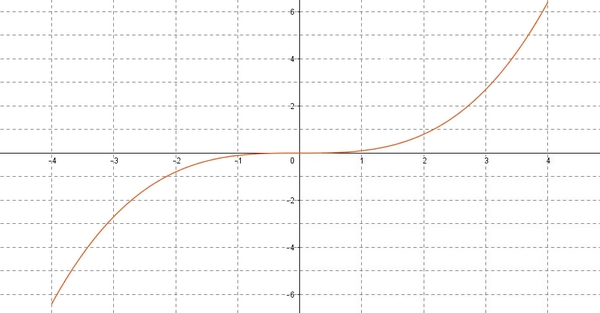
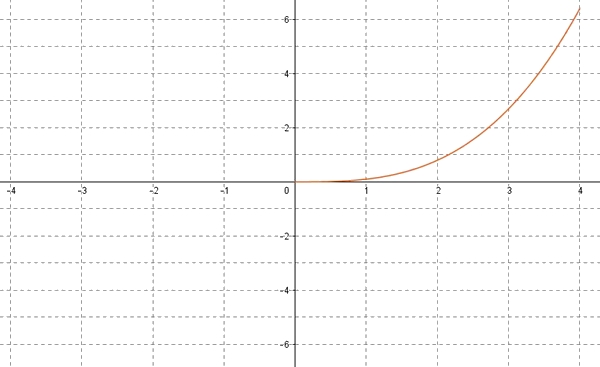
- $f$ est une fonction paire.
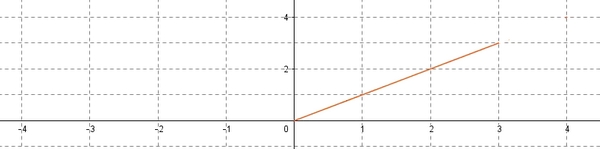
Fonction paire
Une fonction $f$ définie sur $\mathbb{R}$ est paire si pour tout réel $x$ de $D$ on a:
$\begin{cases} -x\in D\\ f(-x)=f(x) \end{cases}$
La représentation graphique de $f$ est alors symétrique par rapport à l'axe des ordonnées.
Remarque: pour tout réel $x\in D$ on a $-x\in D$ signifie que l'ensemble de définition est symétrique par rapport au zéro.
Par exemple si $D=[-3;5]$ la fonction $f$ ne peut pas être paire.Déterminer d'abord l'ensemble de définition de $f$
La courbe est symétrique par rapport à l'axe des ordonnéesPour que l'axe des ordonnées soit un axe de symétrie, on doit avoir $D_f=[-3;3]$
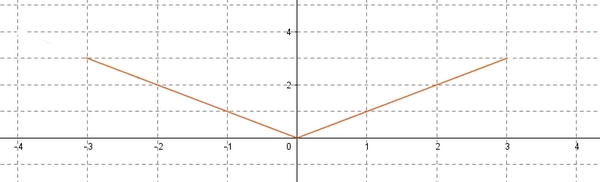
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
