Publications MATHS-LYCEE.FR

mémo+exercices corrigés+liens vidéos

L'essentiel pour réussir la première en spécialité maths

RÉUSSIR EN MATHS, C'EST POSSIBLE!
Tous les chapitres avec pour chaque notion:
- mémo cours
- exercices corrigés d'application directe
- liens vidéos d'explications.
Il est indispensable de maîtriser parfaitement les notions de base et leur application directe pour pourvoir ensuite les utiliser dans la résolution de problèmes plus complexes.

Plus d'infos
  1. spécialité maths terminale
  2. chapitre 8 Géométrie dans l'espace
  3. exercice corrigé nº1328

Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!

Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.
*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
PDF reservé aux abonnés
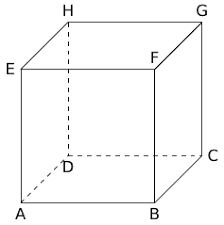
$ABCDEFGH$ est un cube.
  1. Construire le point $M$ tel que $\overrightarrow{AM}=\overrightarrow{EH}+\overrightarrow{AF}$

    Rappel de cours

    relation de Chasles

    $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$

    Aide

    On a $\overrightarrow{EH}=\overrightarrow{FG}$

    Solution

    $\overrightarrow{EH}=\overrightarrow{FG}$
    $\overrightarrow{AM}=\overrightarrow{EH}+\overrightarrow{AF}$
    $\phantom{\overrightarrow{AM}}=\overrightarrow{FG}+\overrightarrow{AF}$
    $\phantom{\overrightarrow{AM}}=\overrightarrow{AF}+\overrightarrow{FG}$
    $\phantom{\overrightarrow{AM}}=\overrightarrow{AG}$
  2. Construire le point $N$ tel que $\overrightarrow{AN}=-\overrightarrow{BC}+\overrightarrow{EG}$

    Rappel de cours

    relation de Chasles

    $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$

    Aide

    On a $\overrightarrow{EG}=\overrightarrow{AC}$

    Solution

    $\overrightarrow{EG}=\overrightarrow{AC}$
    $\overrightarrow{AN}=-\overrightarrow{BC}+\overrightarrow{EG}$
    $\phantom{\overrightarrow{AN}}=\overrightarrow{CB}+\overrightarrow{EG}$
    $\phantom{\overrightarrow{AN}}=\overrightarrow{CB}+\overrightarrow{AC}$
    $\phantom{\overrightarrow{AN}}=\overrightarrow{AC}+\overrightarrow{CB}$
    $\phantom{\overrightarrow{AN}}=\overrightarrow{AB}$
  3. Construire le point $O$ tel que $\overrightarrow{AO}=\overrightarrow{EB}+\overrightarrow{DG}$ puis montrer que $\overrightarrow{AO}=2\overrightarrow{AB}$

    Aide

    $\overrightarrow{EB}=\overrightarrow{EA}+\overrightarrow{AB}$ et $\overrightarrow{DG}=\overrightarrow{DH}+\overrightarrow{HG}$

    Solution

    construction de $\overrightarrow{AO}$

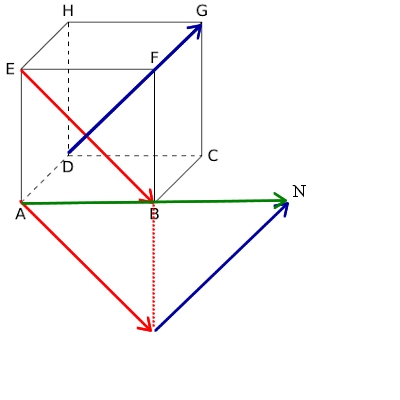
    $\overrightarrow{AO}=\overrightarrow{EB}+\overrightarrow{DG}$
    $\phantom{\overrightarrow{AO}}=\overrightarrow{EA}+\overrightarrow{AB}+\overrightarrow{DH}+\overrightarrow{HG}$
    $\phantom{\overrightarrow{AO}}=\overrightarrow{EA}+\overrightarrow{AB}+\overrightarrow{AE}+\overrightarrow{AB}$ (on a $\overrightarrow{DH}=\overrightarrow{AE}$ et $\overrightarrow{HG}=\overrightarrow{AB}$)
    $\phantom{\overrightarrow{AO}}=\overrightarrow{AB}+\overrightarrow{AB}$
    $\phantom{\overrightarrow{AO}}=2\overrightarrow{AB}$

Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)

exercices semblables


Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
nº1330 Vecteurs colinéaires et alignement
| mn |