Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
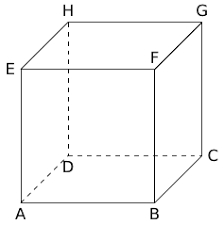
$ABCDEFGH$ est un cube de còté $a$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)

- Calculer $\overrightarrow{AB}.\overrightarrow{AF}$.
produit scalaire
$\overrightarrow{u}$ et $\overrightarrow{v}$ sont deux vecteurs non nuls tels que $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$, le produit scalairedes deux vecteurs est noté \rg{$\overrightarrow{u}.\overrightarrow{v}$},et est le nombre réel défini par:
$\overrightarrow{u}.\overrightarrow{v}=\mid \mid \overrightarrow{u}\mid \mid\times \mid \mid \overrightarrow{v}\mid \mid \times cos(\widehat{BAC})=AB\times AC\times cos(\widehat{BAC})$Produit scalaire avec les projetés orthogonaux
Soit $A$, $B$ et $C$ trois points ($A$ et $B$ distincts) et $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$
Si $H$ est le projeté orthogonal de $C$ sur $(AB)$:
$\overrightarrow{u}.\overrightarrow{v}=AB\times AH$ si $\widehat{BAH}=0$ (soit $\widehat{BAC}$ aigu)
et $\overrightarrow{u}.\overrightarrow{v}=-AB\times AH$ si $\widehat{BAH}=\pi$ (soit $\widehat{BAC}$ obtus)On peut utiliser le projeté orthogonal de $F$ sur $(AB)$ ou bien l'angle $\widehat{BAF}$$ABFE$ est un carré donc le projeté orthogonal de $F$ sur $(AB)$ est $B$
On peut aussi utiliser $\widehat{BAF}$.
$\overrightarrow{AB}.\overrightarrow{AF}=AB\times AF\times cos(\widehat{BAF})=a\times a\sqrt{2}\times \dfrac{\sqrt{2}}{2}=a^2$ (rappel $cos\left(\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}$) - Calculer $\overrightarrow{AB}.\overrightarrow{FE}$.
produit scalaire
$\overrightarrow{u}$ et $\overrightarrow{v}$ sont deux vecteurs non nuls tels que $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$, le produit scalairedes deux vecteurs est noté \rg{$\overrightarrow{u}.\overrightarrow{v}$},et est le nombre réel défini par:
$\overrightarrow{u}.\overrightarrow{v}=\mid \mid \overrightarrow{u}\mid \mid\times \mid \mid \overrightarrow{v}\mid \mid \times cos(\widehat{BAC})=AB\times AC\times cos(\widehat{BAC})$$\widehat{\overrightarrow{AB},\overrightarrow{FE}}=\pi$$\overrightarrow{AB}.\overrightarrow{FE}=AB\times FE\times \cos(\pi)=-a^2$ (rappel $cos(\pi)=-1$
ou bien $\overrightarrow{AB}.\overrightarrow{FE}=\overrightarrow{AB}.\overrightarrow{BA}=\overrightarrow{AB}.(-\overrightarrow{AB})=-AB^2=-a^2$
- Calculer $\overrightarrow{AB}.\overrightarrow{EG}$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
