Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Dans chaque cas, déterminer sir les points $A$ et $B$ associés aux réels $a$ et $b$ sur le cercle trigonométriques sont confondus.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
- $a=\dfrac{\pi}{6}$ et $b=\dfrac{5\pi}{6}$
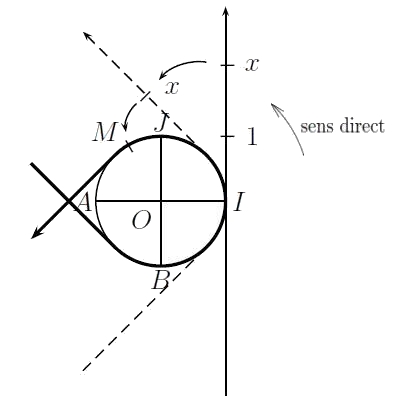
Lien droite réelle et cercle trigonométrique
Soit $\mathcal{C}$ le cercle trigonométrique. A tout réel $x$ on associe un point $M$ unique de $\mathcal{C}$ de la manière suivante :
- Si $x \geq 0$ on parcourt le cercle dans le sens direct en partant de $I$ jusqu'à avoir parcouru la longueur $x$.
- Si $x \leq 0$ on parcourt le cercle dans le sens indirect en partant de $I$ jusqu'à avoir parcouru la longueur $|x|$.
 Un tour complet sur le cercle trigonométrique correspond au réel $2\pi$$b-a=\dfrac{5\pi}{6}-\dfrac{\pi}{6}$
Un tour complet sur le cercle trigonométrique correspond au réel $2\pi$$b-a=\dfrac{5\pi}{6}-\dfrac{\pi}{6}$
$~~~~~~=\dfrac{4\pi}{6}$
$~~~~~~=\dfrac{2\pi}{3}$
La différence entre $a$ et $b$ n'est pas un multiple de $2\pi$
- $a=\dfrac{17\pi}{4}$ et $b=\dfrac{-7\pi}{4}$
- $a=\dfrac{-12\pi}{5}$ et $b=\dfrac{3\pi}{5}$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
