Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Résoudre les équations suivantes dans $\mathbb{R}$.
On pourra utiliser le cercle trigonométrique.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
On pourra utiliser le cercle trigonométrique.
- $2cos(x)=-1$
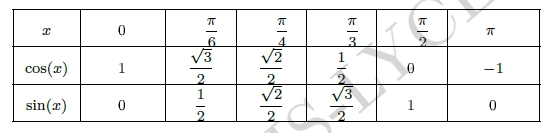
Valeurs remarquables du cos et du sin
 Isoler $cos(x)$
Isoler $cos(x)$
Chercher une valeur de $\alpha$ telle que $cos(\alpha)=\dfrac{1}{2}$.
Utiliser le cercle trigonométrique et les symétries par rapport aux axes du repère et par rapport à l'origine pour déterminer les valeurs de $x$
il y a deux valeurs de $x$ donnant le même cosinus$2cos(x)=-1 \Longleftrightarrow cos(x)=\dfrac{-1}{2}$
$cos(\dfrac{\pi}{3})=\dfrac{1}{2}$
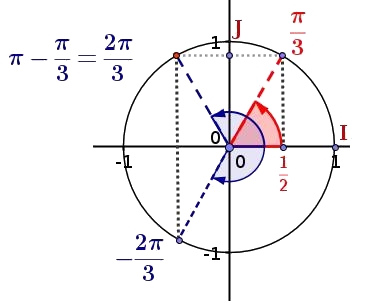
$cos(\dfrac{2\pi}{3})=cos(\dfrac{-2\pi}{3})=-\dfrac{1}{2}$
On résout dans $\mathbb{R}$
- $2cos(x)+1=2$
Isoler $cos(x)$
Chercher une mesure $\alpha$ telle que $cos(\alpha)=\dfrac{1}{2}$
En déduire les valeurs pour lesquelles $cos(x)=\dfrac{1}{2}$
il y a deux valeurs de $x$ donnant le même cosinus$2cos(x)+1=2 \Longleftrightarrow cos(x)=\dfrac{1}{2}$
$cos(\dfrac{\pi}{3})=\dfrac{1}{2}$
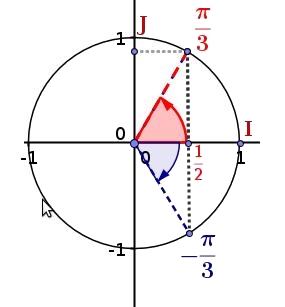
$cos(\dfrac{\pi}{3})=cos(\dfrac{-\pi}{3})=\dfrac{1}{2}$
On résout dans $\mathbb{R}$
- $cos(x)=\dfrac{-1}{\sqrt{2}}$
Ecrire le membre de gauche sans racine carrée au dénominateur
Chercher une mesure $\alpha$ telle que $cos(\alpha)=\dfrac{\sqrt{2}}{2}$
Utiliser le cercle trigonométrique et les symétries par rapport aux axes du repère et par rapport à l'origine pour déterminer les valeurs de $x$
il y a deux valeurs de $x$ donnant le même cosinus$cos(x)=\dfrac{-1}{\sqrt{2}} \Longleftrightarrow cos(x)=\dfrac{-\sqrt{2}}{\sqrt{2}\sqrt{2}}\Longleftrightarrow cos(x)=\dfrac{-\sqrt{2}}{2}$
$cos(\dfrac{\pi}{4})=\dfrac{\sqrt{2}}{2}$
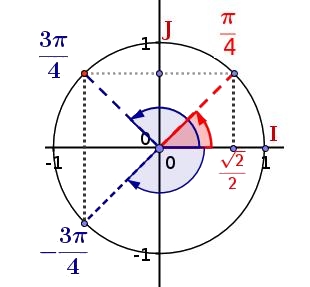
$cos(\dfrac{3\pi}{4})=cos(\dfrac{-3\pi}{4})=-\dfrac{\sqrt{2}}{2}$
On résout dans $\mathbb{R}$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
