Publications MATHS-LYCEE.FR
Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
$ABCDEFGH$ est un pavé droit.
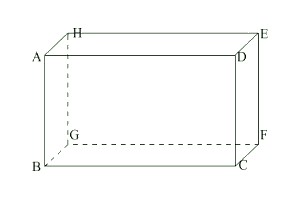
Donner la position relative des droites suivantes:
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Donner la position relative des droites suivantes:
- $(AB)$ et $(EF)$
Position relative de deux droites
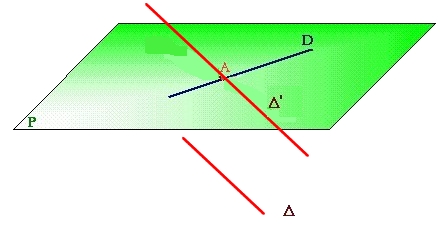
- Les droites $D$ et $\Delta$
Les droites $D$ et $\Delta$ ne sont pas coplanaires
Aucun plan ne contient les deux droites
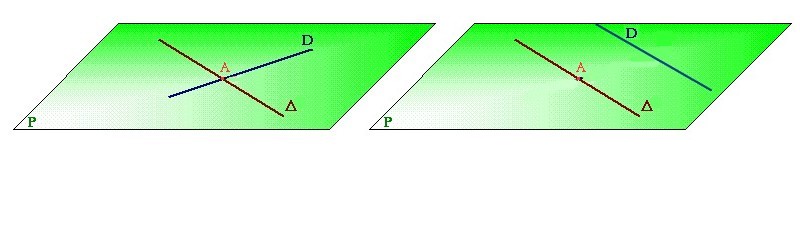
Les droites $D$ et $\Delta$
Les droites $D$ et $\Delta$ ne sont pas coplanaires Les deux droites sont sécantes ou parallèles
On peut utiliser les faces $(ABC)$ et $(CDE)$
ou bien que les faces $(ABC)$ et $(GFE)$ sont parallèles$ABCD$ est un rectangle donc $(AB)//(CD)$
et $CDEF$ est un rectangle donc $(CD)//(EF)$
On a $(AB)//(CD)$ et $(CD)//(EF)$
- $(AB)$ et $(DH)$
Position relative d'une droite et d'un plan
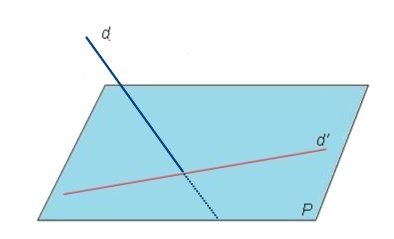
La droite $d$ et le plan $P$ sont sécants
L'intersection est un point
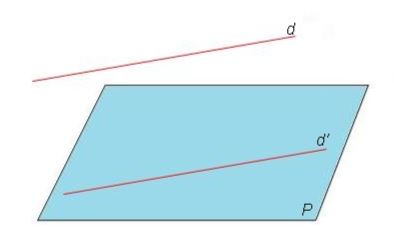
La droite $d$ et le plan $P$ sont parallèles
Il existe une droite de $P$ parallèle à $d$
La droite $(AB)$ est parallèle à la droite $(HG)$ qui est incluse dans le plan $(DHG)$
$(DH)$ est contenue dans le plan $(DHG)$$ABGH$ est un rectangle donc $(AB)$ est parallèle à $(GH)$
donc $(AB)$ est parallèle au plan $(DHG)$ et la droite $(DH)$ est contenue dans le plan $(DHG)$
- $(HC)$ et $(BE)$
On peut utiliser le plan $(EHB)$$H$ et $C$ appartiennent au plan $(HCE)$ donc $(HC)$ est contenue dans $(HEC)$.
$(BC)//(HE)$ et le plan $(HEC)$ est confondu avec le plan $(BCE)$ donc $(BE)$ est contenue dans $(HCE)$.
Les droites $(HC)$ et $(BE)$ sont contenues dans le plan $(HCE)$ et ne sont pas parallèles
On a $\overrightarrow{BC}=\overrightarrow{AD}=\overrightarrow{HE}$ donc $BCEH$ est un parallélogramme dont les diagonales sont $(BE)$ et $(HC)$ et ces deux droites sont donc sécantes.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.