Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
$a$ est un nombre compris entre $0$ et $1$.
On veut comparer un réel $a$ et son carré.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
On veut comparer un réel $a$ et son carré.
- Approche graphique ( si le chapitre fonction a été traité)
On donne c-dessous la représentation graphique de la fonction carré soit $f(x)=x^2$ sur $[0;+\infty[$
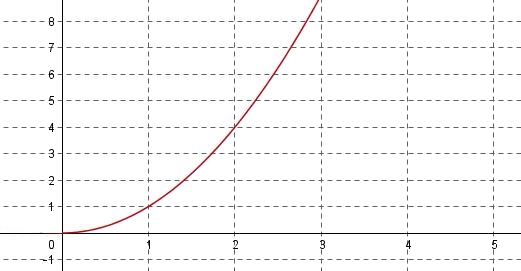
- Pour $x\geq 0$, tracer la représentation graphique de la fonction linéaire $g$ définie par $g(x)=x$.
Fonction affine
Une fonction afffine est définie sur $\mathbb{R}$ par $f(x)=ax+b$.
La représentation graphique d'une fonction affine est une droite coupant l'axe des ordonnées au point $(0;b)$ et l'axe des abscisses au point $\left(\dfrac{-b}{a}\right)$ (si $a\neq 0$).
Si $a=0$ alors la droite est parallèle à l'axe des abscisses.La représentation graphique de $g$ est une droitePour tracer la droite représentant $g$ on peut utiliser deux points de la droite:
si $x=0$ alors $g(0)=0$ et si $x=2$ alors $g(2)=2$
La droite représentant $g$ passe par l'origine du repère et par $A(2;2)$.
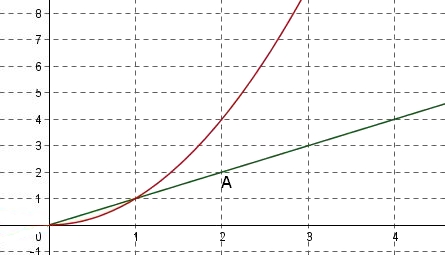
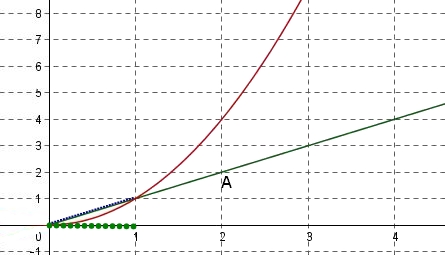
- Déterminer graphiquement les valeurs de $x$ pour lesquelles on a $x> x^2$.
- Que peut-on dire de $x$ et de $x^2$ quand $x> 1$?
- Pour $x\geq 0$, tracer la représentation graphique de la fonction linéaire $g$ définie par $g(x)=x$.
- Comparaison par le calcul
Pour $a>0$, comparer $a$ et $a^2$ en fonction des valeurs prises par $a$.
On pourra factoriser l'expression obtenue en calculant la différence.Comparer deux nombres
Soit $a$ et $b$ deux nombres réels, $a < b$ si et seulement si $b-a>0$
Conséquence: Pour comparer deux nombres ou deux expressions, on peut étudier le signe de leur différence.Il faut étudier le signe de $a^2-a$ en factorisant l'expressionPour comparer $a^2$ et $a$, on peut étudier le signe de la différence entre ces deux nombres.
$a^2-a=a(a-1)$
On a $a > 0$ et donc deux cas possibles:
- cas où $a < 1$
On a donc $a-1 < 0$ et $a >0$ donc $a(a-1)$ est de signe négatif
donc $a^2-a < 0$ soit $a^2 < a$
- cas où $a > 1$
On a donc $a-1 > 0$ et $a > 0$
donc $a^2-a > 0$ soit $a^2 > a$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.