Publications MATHS-LYCEE.FR
Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
On veut résoudre l'inéquation $x^3-x^2-9x+9\geq 0$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
- Montrer que pour tout réel $x$, on a $x^3-x^2-9x+9=(x-1)(x^2-9)$
- Factoriser alors au maximum $x^3-x^2-9x+9$
Identités remarquables
$(a+b)^2=a^2+2ab+b^2$
$(a-b)^2=a^2-2ab+b^2$
$(a-b)(a+b)=a^2-b^2$
On peut utiliser la troisième identité remarquable pour factoriser $x^2-9$$x^3-x^2-9x+9=(x-1)(x^2-9)$
$\phantom{x^3-x^2-9x+9}=(x-1)(x^2-3^2)$
$\phantom{x^3-x^2-9x+9}=(x-1)(x-3)(x+3)$
$\phantom{x^3-x^2-9x+9}=(x-1)(x-3)(x+3)$
- Résoudre alors l'inéquation $x^3-x^2-9x+9\geq 0$
Utiliser la forme factorisée pour dresser un tableau de signes $x^3-x^2-9x+9$$x^3-x^2-9x+9\geq 0 \Longleftrightarrow (x-1)(x-3)(x+3)\geq 0$
$x-1$ s'annule pour $x_1=1$
$x-3$ s'annule pour $x_2=3$
$x+3$ s'annule pour $x=-3$
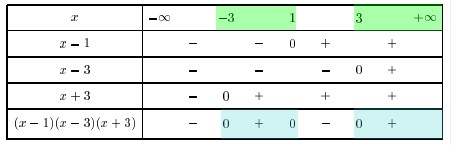
On a donc $(x-1)(x-3)(x+3)\geq 0$ (zone bleue) pour $x\in [-3;1]\cup [3;+\infty[$ (zone verte)
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
nº261 Signe d'un produit de trois facteurs
| 4-8mn |
nº262 Inéquation avec trois facteurs
| 8-12mn |
| 4-8mn |
nº262 Inéquation avec trois facteurs
| 8-12mn |