Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Inscrivez vous gratuitement ici....
Contenu
Ensemble de définition et tableau de variation à partir du graphique avec une valeur interdite
Ressources associées et exercices semblables
représentation graphique à partir d’un tableau de variation (réf 0208)
exercice
Vidéo de l’exercice
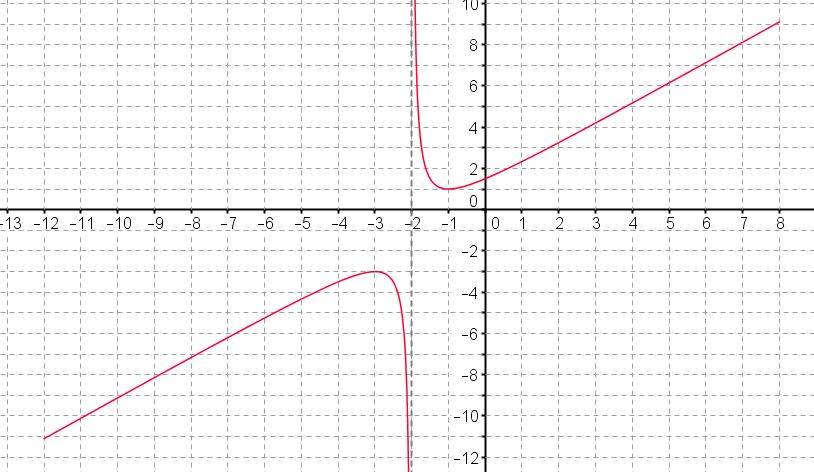
- Peut-on déterminer l'image de $-2$ par $f$?
En déduire l'ensemble de définition $D_f$ de $f$.
Rappel cours
Ensemble de définition
L'ensemble de définition d'une fonction $f$ est l'ensemble des valeurs pour lesquelles on peut calculer l'image par $f$.
Par exemple, l'ensemble de définition de la fonction $f$ définie par $f(x)=\dfrac{1}{x+2}$ est $\mathbb{R}\setminus \lbrace -2\rbrace$ car le dénominateur doit être différent de $0$.Aide
La courbe est "coupée" au niveau de la droite tracée en pointillés gris.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Dresser le tableau de variations de $f$.
Rappel cours
Tableau de variation avec valeur interdite
$f$ est une fonction définie sur un intervalle I de $\mathbb{R}$ et $C_f$ sa représentation graphique.
Le tableau de variation de $f$ permet de visualiser les variations de $f$ ainsi que ses extremums (maximum ou minimum).
Une double barre signifie que la fonction n'est pas définie.
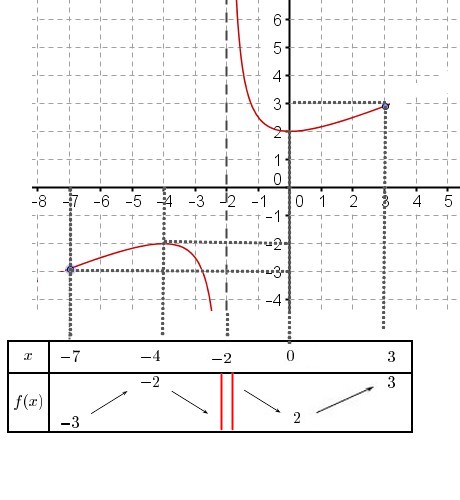
Aide
Il faut déterminer les valeurs de $x$ pour lesquelles la fonction change de sens de variation.
ne pas oublier la valeur interditeSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message