Envoyez votre messageInfos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Compléter le tableau de variation d’une fonction paire ou impaire
Ressources associées et exercices semblables
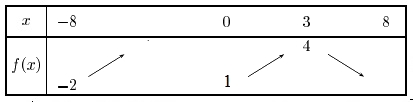
- $f$ est une fonction paire.
Rappel cours
Fonction paire
Une fonction $f$ définie sur $\mathbb{R}$ est paire si pour tout réel $x$ de $D$ on a:
$\begin{cases} -x\in D\\ f(-x)=f(x) \end{cases}$
La représentation graphique de $f$ est alors symétrique par rapport à l'axe des ordonnées.
Remarque: pour tout réel $x\in D$ on a $-x\in D$ signifie que l'ensemble de définition est symétrique par rapport au zéro.
Par exemple si $D=[-3;5]$ la fonction $f$ ne peut pas être paire.Aide
si $f$ est croissante sur $[0;3]$, par symétrie, la fonction est décroissante sur $[-3;0]$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
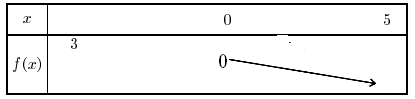
INSCRIPTION - $f$ est une fonction impaire.
Rappel cours
Fonction impaire
Une fonction $f$ définie sur $\mathbb{R}$ est impaire si pour tout réel $x$ de $D$ on a:
$\begin{cases} -x\in D\\ f(-x)=-f(x) \end{cases}$
La représentation graphique de $f$ est alors symétrique par rapport à l'origine du repère.
Remarque: pour tout réel $x\in D$ on a $-x\in D$ signifie que l'ensemble de définition est symétrique par rapport au zéro.
Par exemple si $D=[-3;5]$ la fonction $f$ ne peut pas être impaire.Aide
si $f$ est décroissante sur $[0;5]$, par symétrie, la fonction est décroissante sur $[-5;0]$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
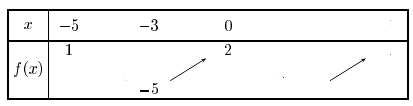
INSCRIPTION - $f$ est une fonction paire.
Aide
si $f$ est croissante sur $[-3;0]$, par symétrie, la fonction est décroissante sur $[0;3]$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
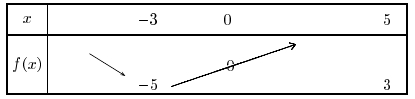
INSCRIPTION - $f$ est une fonction impaire.
Aide
si $f$ est décroissante sur $[-5;-3]$, par symétrie, la fonction est décroissante sur $[3;5]$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION