Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Déterminer une équation cartésienne
Problème d’alignement utilisant un repère
Équation cartésienne avec un paramètre
Ressources associées et exercices semblables
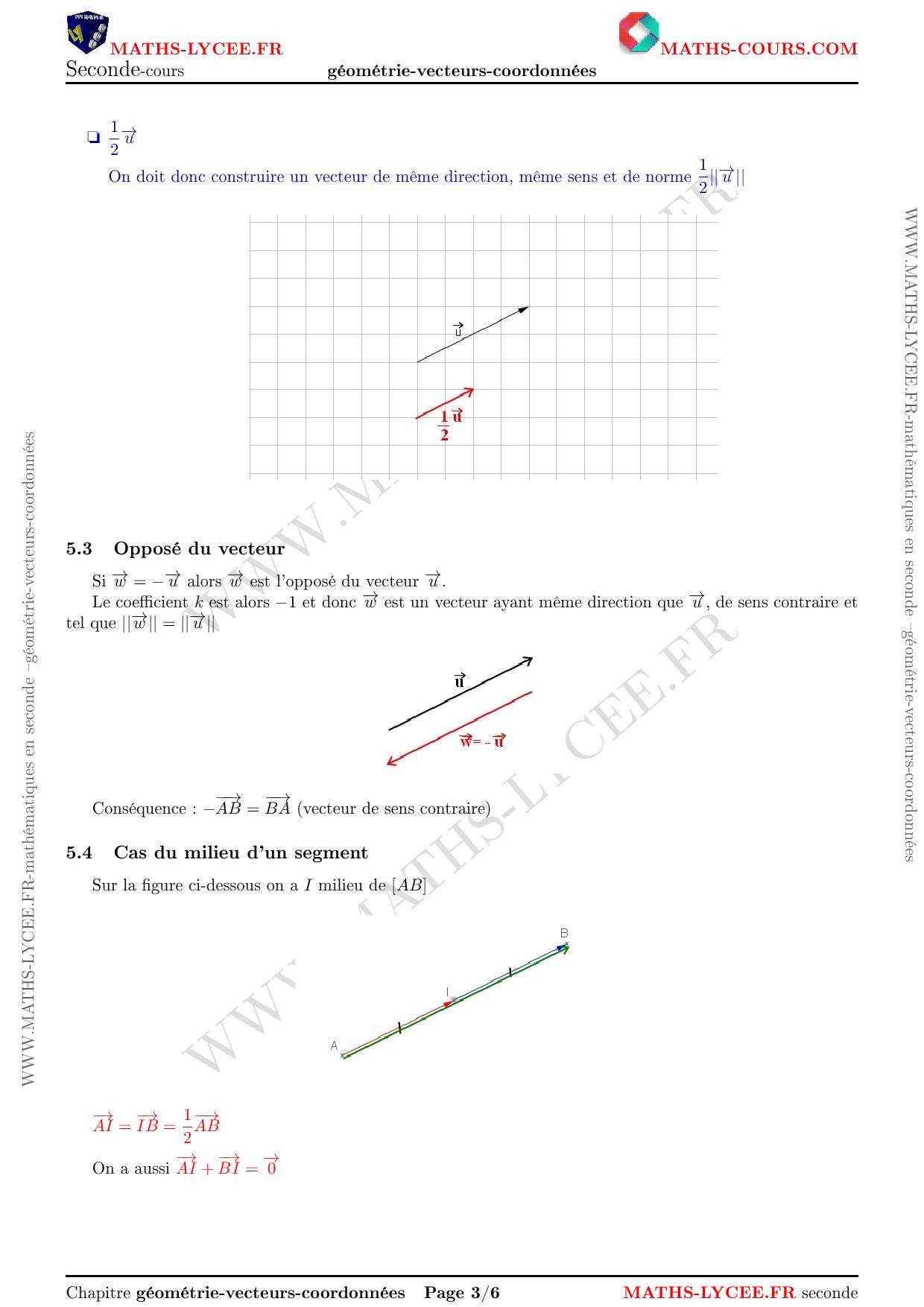
- Dans le repère ci-dessous, tracer $(d)$, placer $A$ et construire $\overrightarrow{v}$.

Rappel cours
Tracer une droite
Pour tracer une droite donnée par une équation cartésienne, on peut:
1. choisir deux valeurs de $x$ et calculer l'ordonnée correspondante avec l'équation de $(d)$ et placer les deux points obtenus
2. utiliser un vecteur directeur de $(d)$ et calculer l'ordonnée d'un point de $(d)$ en choisissant une valeur de $x$Aide
Pour tracer une droite, il faut chercher les coordonnées de deux points de cette droite
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Donner les coordonnées d'un vecteur directeur $\overrightarrow{u}$ de $(d)$.
Rappel cours
Vecteur directeur dans un repère
Dans un repère du plan, la droite $(d)$ a pour équation cartésienne $ax+by+c=0$ alors $\overrightarrow{u}\begin{pmatrix}-b\\a\end{pmatrix}$ est un vecteur directeur de $(d)$.
Si $(d)$ est définie par son équation réduite $y=ax+b$, $\overrightarrow{u}\begin{pmatrix}1\\a\end{pmatrix}$ est un vecteur directeur de $(d)$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Construire le vecteur $\overrightarrow{w}$ (laisser les traces de la construction) défini par $\overrightarrow{w}=2\overrightarrow{u}-\dfrac{1}{2}\overrightarrow{v}$.
Calculer ensuite les coordonnées de $\overrightarrow{w}$.Aide
Traduire cette égalité vectorielle avec les abscisses puis les ordonnées des vecteurs
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $\overrightarrow{v}$ et $\overrightarrow{w}$ sont-ils colinéaires?
Rappel cours
Critère de colinéarité dans un repère
Dans un repère du plan, $\overrightarrow{u}(x;y)$ et $\overrightarrow{w}(x'y')$ non nuls sont colinéaires si et seulement si $xy'-x'y=0$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer une équation cartésienne de la droite $(d')$ passant par $A$ et de vecteur directeur $\overrightarrow{v}$ puis la tracer.
Rappel cours
Déterminer une équation cartésienne
Déterminer une équation cartésienne de la droite $(AB)$ avec $A(x_A;y_A)$ et $B(x_B;y_B)$ donnés dans un repère.
Méthode 1
- calculer les coordonnée du vecteur $\overrightarrow{AB}$ vecteur directeur de $(AB)$
- Si le point $M(x;y)$ appartient à $(AB)$, les vecteurs $\overrightarrow{AM}$ et $\overrightarrow{AB}$ sont colinéaires
- $det(\overrightarrow{AM};\overrightarrow{AB})=0$
Méthode 2
- calculer les coordonnée du vecteur $\overrightarrow{AB}$ vecteur directeur de $(AB)$
- Les coordonnées de $\overrightarrow{AB}\begin{pmatrix}-b\\a\end{pmatrix}$ donnent les coefficients $a$ et $b$ d'une équation cartésienne
- $(AB)$: $ax+by+c=0$ et $A\in (AB)$ donc $ax_A+by_A+c=0$ (équation d'inconnue $c$)Aide
Un point $M(x;y)$ appartient à la droite $(d')$ si et seulement si les vecteurs $\overrightarrow{AM}$ et $\overrightarrow{v}$ sont colinéaires
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer les coordonnées du point d'intersection de $(d)$ et $(d')$.
Aide
Il faut résoudre le système formé avec une équation de chacune des droites
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer une équation cartésienne de la droite $(d'')$ parallèle à $(d)$ passant par $A$ puis tracer $(d'')$.
Rappel cours
Droites parallèles
Deux droites parallèles ont des vecteurs directeurs colinéaires (ayant la même direction)Aide
Un point $M(x;y)$ appartient à $(d'')$ si et seulement si le vecteur $\overrightarrow{AM}$ est colinéaire à un vecteur directeur de $(d)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
I est le milieu de $[AG]$ et J est le point d'intersection de $(AE)$ et $(BG)$.
Montrer que $C$, $I$ et $J$ sont alignés.
On pourra utiliser le repère orthonormé $(A;\overrightarrow{AB};\overrightarrow{AH})$.
Aide
On a alors dans ce repère $B(1;0)$, $G(1;1)$, $E(3;1)$ et $C(2;0)$
Il faut ensuite déterminer une équation de la droite $(AE)$ pour déterminer ensuite l'ordonnée de $J$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
On considère l'ensemble $D_m$ des points $M(x;y)$ dont les coordonnées vérifient
la relation $mx+(2m-1)y+4=0$, avec $m$ réel.
- Montrer que l'ensemble $D_m$ est une droite.
Aide
Toute droite admet une équation de la forme $ax+by+c=0$ dans un repère du plan avec $(a;b)\neq(0;0)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Pour quelles valeurs de $m$ $D_m$ est-elle parallèle à l'un des axes du repère?
Rappel cours
Vecteur directeur dans un repère
Dans un repère du plan, la droite $(d)$ a pour équation cartésienne $ax+by+c=0$ alors $\overrightarrow{u}\begin{pmatrix}-b\\a\end{pmatrix}$ est un vecteur directeur de $(d)$.
Si $(d)$ est définie par son équation réduite $y=ax+b$, $\overrightarrow{u}\begin{pmatrix}1\\a\end{pmatrix}$ est un vecteur directeur de $(d)$.
Aide
Si les vecteurs directeurs de $(D_m)$ ont pour abscisse $0$ alors $(d_m)$ est parallèle à l'axe des ordonnées
Si les vecteurs directeurs de $(D_m)$ ont pour ordonnée $0$ alors $(d_m)$ est parallèle à l'axe des abscissesSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Donner une équation des droites $D_0$ et $D_1$ puis déterminer les coordonnées de leur point d'intersection.
Aide
0 Remplacer $m$ par 0 puis $m$ par 1 dans $mx+(2m-1)y+4=0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Montrer que $D_m$ passe par un point fixe quelque soit la valeur du réel $m$.
Aide
11 Les droites $D_0$ et $D_1$ sont sécantes en I donc il suffit de vérifier que I appartient à la droite $D_m$ quelque soit la valeur de $m$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message