Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Déterminer la forme canonique
Dresser le tableau de variation
Discriminant et racines
Équations du second degré avec un quotient
Ressources associées et exercices semblables
Devoir forme canonique, racines et discriminant et équations de degré 2 (réf 0513)
devoir
- $P(x)=2x^2-4x-1$
Rappel cours
Forme canonique
Toute fonction polynôme de degré 2 définie sur $\mathbb{R}$ par $P (x) = ax^2 + bx + c$ peut s'écrire sous la forme $P (x) = a(x -\alpha)^2 + \beta$ avec $\alpha=\dfrac{-b}{2a}$ et $\beta= P ( \alpha)$.
Cette écriture de $P (x)$ est appelée forme canonique et $S(\alpha;\beta)$ est le sommet de la parabole représentant la fonction $P$ Variations fonction polynôme du second degré
Soit la fonction $P$ définie sur $\mathbb{R}$ par sa forme canonique $P (x) = a(x-\alpha)^2 + \beta$
La courbe représentative de $P$ est une parabole dont le sommet a pour coordonnées $(\alpha; \beta)$.
Tableau de variation: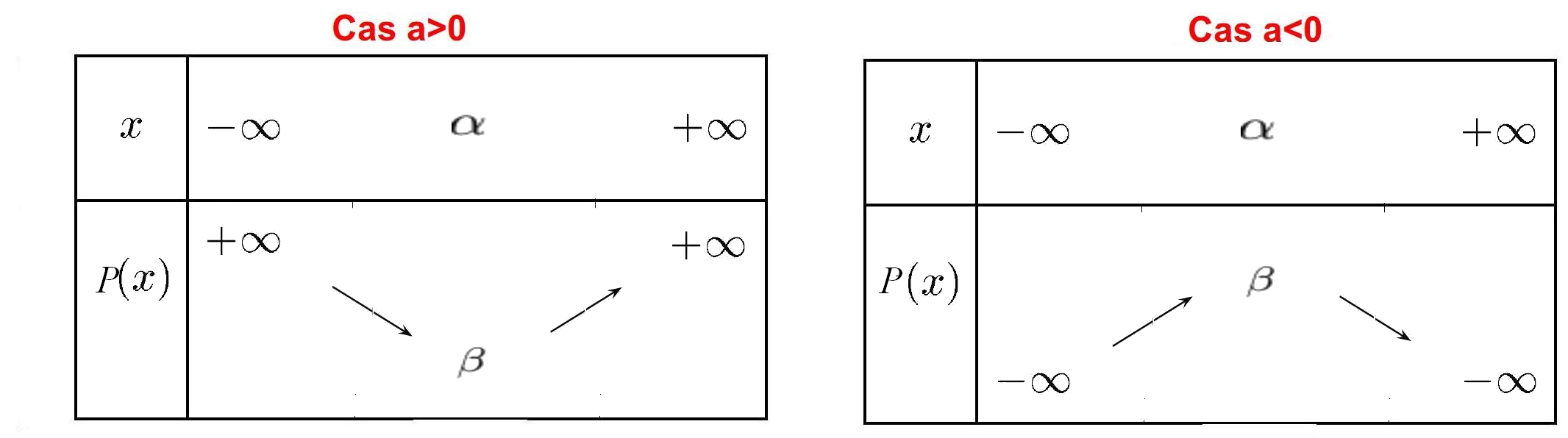
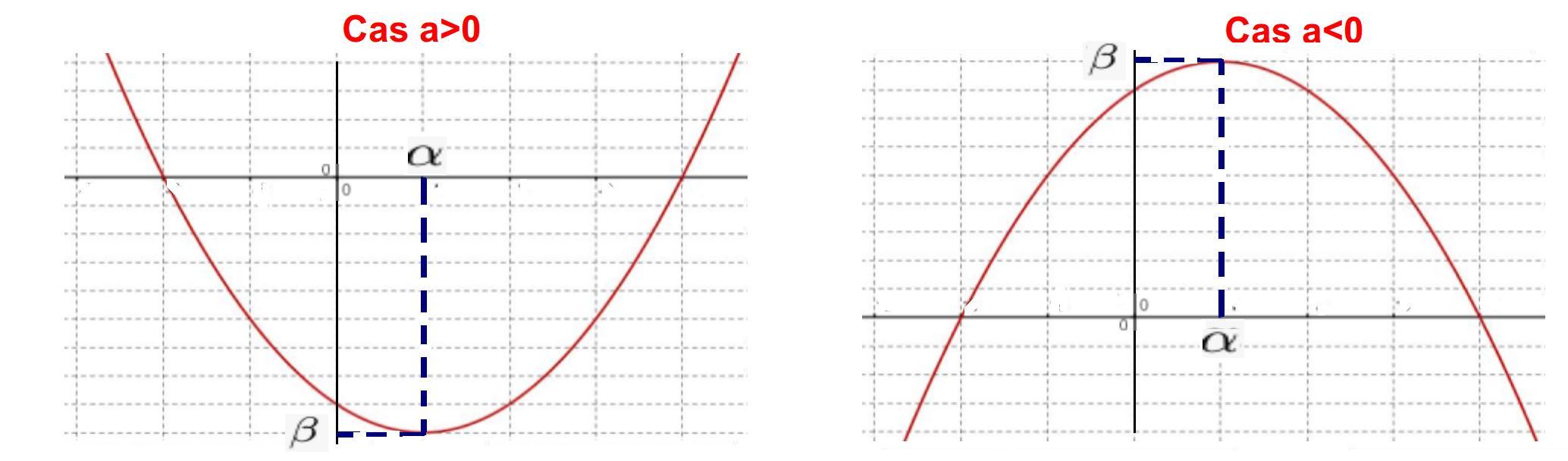
Aide
Calculer $\alpha$ et $f(\alpha)$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - $P(x)=3+x^2+2x$
Aide
écrire le polynôme en ordonnant selon les puissances décroissantes de $x$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION
- $2x^2-8x-24=0$
Rappel cours
Discriminant
$P(x)=ax^2+bx+c$ avec $a\neq 0$.
Le discriminant du polynôme du second degré $P$ est $\Delta=b^2-4ac$Aide
Calculer le discriminant $\Delta$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - $(2x-1)(x-3)=4x-9$
Aide
Développer, simplifier et se ramener +a une équation de la forme $ax^2+bx+c=0$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION
Une entreprise vend des paquets de biscuits et le bénéfice journalier de cette entreprise, en euros, est donné par la fonction $B$ définie sur $[0;300]$ par $B(x)=-x^2+103x+100$ où $x$ est la quantité de paquets produite, exprimée en centaines de paquets.
Déterminer le nombre de paquets à produire chaque jour pour que le bénéfice soit maximum et le montant des bénéfices correspondant à cette quantité.
Rappel cours
Forme canonique
Toute fonction polynôme de degré 2 définie sur $\mathbb{R}$ par $P (x) = ax^2 + bx + c$ peut s'écrire sous la forme $P (x) = a(x -\alpha)^2 + \beta$ avec $\alpha=\dfrac{-b}{2a}$ et $\beta= P ( \alpha)$.
Cette écriture de $P (x)$ est appelée forme canonique et $S(\alpha;\beta)$ est le sommet de la parabole représentant la fonction $P$
Variations fonction polynôme du second degré
Soit la fonction $P$ définie sur $\mathbb{R}$ par sa forme canonique $P (x) = a(x-\alpha)^2 + \beta$
La courbe représentative de $P$ est une parabole dont le sommet a pour coordonnées $(\alpha; \beta)$.
Tableau de variation:


Aide
Il faut déterminer la forme canonique de $B(x)$ et dresser sson tableau de variation
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION


 Envoyez votre message
Envoyez votre message