Envoyez votre messageInfos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Utilisation de la relation $cos^2(x)+sin^2(x)=1$
Calcul du sinus connaissant le cosinus
Calcul du cosinus et du sinus avec les angles associés
Ressources associées et exercices semblables
Utilisation de la formule cos^2(x) sin^2(x)=1 pour calculer cos ou sin (réf 0719)
exercice
- En déduire $sin(\dfrac{2\pi}{5})$
Rappel cours
Identités remarquables
$(a+b)^2=a^2+2ab+b^2$
$(a-b)^2=a^2-2ab+b^2$
$(a-b)(a+b)=a^2-b^2$
Aide
On utilise $cos^2(x)+sin^2(x)=1$
$x \in [0;\pi[$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Calculer $cos(\dfrac{7\pi}{5})$
Rappel cours
Angles associés
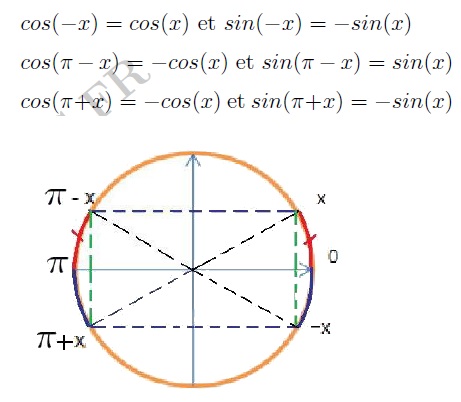
Aide
$\dfrac{7\pi}{5}=\pi+\dfrac{2\pi}{5}$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer ensuite $cos(\dfrac{\pi}{10})$
Aide
$\dfrac{\pi}{2}-\dfrac{2\pi}{5}=\dfrac{5\pi}{10}-\dfrac{4\pi}{10}=\dfrac{\pi}{10}$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements