Envoyez votre messageInfos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Équations avec cosinus sur $]-\pi;pi]$
Mesure principale des solutions
Ressources associées et exercices semblables
Équations avec cosinus (réf 0727)
exercice
Équations avec sinus (réf 0728)
exercice
On pourra utiliser le cercle trigonométrique.
- $cos(x)=\dfrac{1}{2}$
Rappel cours
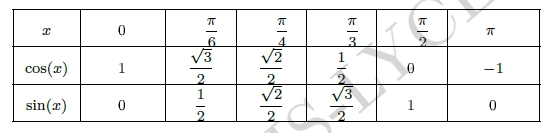
Valeurs remarquables du cos et du sin
Aide
Chercher une mesure $\alpha$ telle que $cos(\alpha)=\dfrac{1}{2}$
il y a deux valeurs de $x$ possibles donnant le même cosinusSolution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - $cos(x)=\dfrac{-\sqrt{3}}{2}$
Aide
Chercher une mesure $\alpha$ telle que $cos(\alpha)=\dfrac{\sqrt{3}}{2}$
En déduire les valeurs pour lesquelles $cos(x)=-\dfrac{\sqrt{3}}{2}$
Pour tout réel $x$, on a $cos(-x)=cos(x)$Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - $cos(x)=\dfrac{\sqrt{2}}{2}$
Aide
Chercher une mesure $\alpha$ telle que $cos(\alpha)=\dfrac{\sqrt{2}}{2}$
Pour tout réel $x$, on a $cos(-x)=cos(x)$Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION